“五米三向折返跑”的成绩反映了人体的灵敏素质。测定时,受试者听到口令后起跑,测试员同时开始计时,受试者从起点A全力跑向5m处的B点用手触摸折返线处后返回A点,然后依次到C点、D点最终返回A点。所用时间即为“五米三向折返跑”的成绩。现测得 受试者成绩为7.50s,该受试者在测试全过程中的路程和平均速度的大小分别为( )
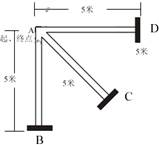
| A.0,0 | B.15,4m/s | C.30m,0 | D.30m,4m/s |
如图,分别用力F1、F2、F3将质量为m的物体由静止沿同一固定光滑斜面以相同的加速度从斜面底端拉到斜面的顶端,在此过程中,F1、F2、F3做功的功率大小关系是()
| A.P1=P2=P3 | B.P1>P2=P3 | C.P3>P2>P1 | D.P1>P2>P3 |
如图所示,下列四个选项的图中,木块均在固定的斜面上运动,其中图A、B、C中的斜面是光滑的,图D中的斜面是粗糙的,图A、B中的F为木块所受的外力,方向如图中箭头所示,图A、B、D中的木块向下运动.图C中的木块向上运动.在这四个图所示的运动过程中机械能守恒的是( )
如图所示,A、B两小球在光滑水平面上分别以动量p1=4kg·m/s和p2=6kg·m/s(向右为参考正方向)做匀速直线运动,则在A球追上B球并与之碰撞的过程中,两小球的动量变化量Δp1和Δp2可能分别为()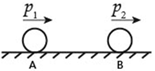
A.-2kg·m/s,3kg·m/s
B.-8kg·m/s,8kg·m/s
C.1kg·m/s,-1kg·m/s
D.-2kg·m/s,2kg·m/s
冰面对溜冰运动员的最大静摩擦力为运动员重力的k倍,在水平冰面上沿半径为R的圆周滑行的运动员,其安全速度为( )
A.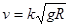 |
B.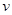 ≤ ≤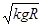 |
C.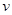 ≥ ≥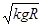 |
D.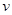 ≤ ≤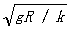 |
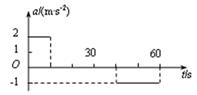
汽车由静止开始在平直的公路上行驶,0~60s内汽车的加速度随时间变化的图像如图2所示。则该汽车在0~60s内的速度-时间图像(即v-t图像)为图3中的()