某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．
解不等式10-4（x-4）≤2（x-1），并把它的解集在数轴上表示出来．
如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标（3，3），将正方形ABCO绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG．
（1）求证：△AOG≌△ADG；
（2）求∠PAG的度数；并判断线段OG、PG、BP之间的数量关系，说明理由；
（3）当∠1=∠2时，求直线PE的解析式．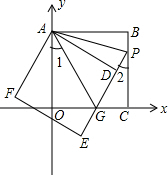
如图（1），在矩形ABCD中，把∠B、∠D分别翻折，使点B、D恰好落在对角线AC上的点E、F处，折痕分别为CM、AN，
（1）求证：△ADN≌△CBM；
（2）请连接MF、NE，证明四边形MFNE是平行四边形；四边形MFNE是菱形吗？请说明理由；
（3）点P、Q是矩形的边CD、AB上的两点，连接PQ、CQ、MN，如图（2）所示，若PQ=CQ，PQ∥MN，且AB=4cm，BC=3cm，求PC的长度．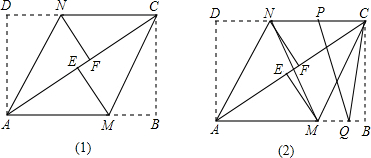
某饮料厂开发了A、B两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示．现用甲原料和乙原料各2800克进行试生产，计划生产A、B两种饮料共100瓶．设生产A种饮料x瓶，解析下列问题：
| 原料名称饮料名称 |
甲 |
乙 |
| A |
20克 |
40克 |
| B |
30克 |
20克 |
（1）有几种符合题意的生产方案写出解析过程；
（2）如果A种饮料每瓶的成本为2.60元，B种饮料每瓶的成本为2.80元，这两种饮料成本总额为y元，请写出y与x之间的关系式，并说明x取何值会使成本总额最低？
关于x的不等式组
恰有两个整数解．则实数a的取值范围为 .