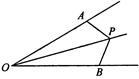
某学校游戏节活动中,设计了一个有奖转盘游戏,如图,A转盘被分成三个面积相等的扇形,B转盘被分成四个面积相等的扇形,每一个扇形都标有相应的数字,先转动A转盘,记下指针所指区域内的数字,再转动B转盘,记下指针所指区域内的数字(当指针在边界线上时,重新转动转盘,直到指针指向一个区域内为止)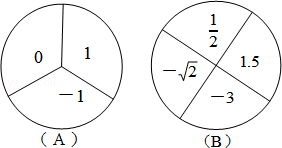
(1)请利用画树状图或列表的方法(只选其中一种),表示出转转盘可能出现的所有结果;
(2)如果将两次转转盘指针所指区域的数据相乘,乘积是无理数时获得一等奖,那么获得一等奖的概率是多少?
如图,某铁路MN和公路PQ相交于点O,且交角为90°,某仓库G在A区,到公路、铁路距离相等(即G在∠NOQ的平分线上),且到公路与铁路的相交点O的距离为200m.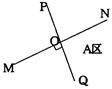
(1)在图上标出仓库G的位置(比例尺1∶10000,用圆规作图,保留作图痕迹,不写作法):
(2)求出仓库G到铁路的实际距离.
△ABC中,AB=BC=CA,三内角平分线交于O,OP⊥AB于P,OM⊥BC于M,ON⊥CA于N,AH⊥BC于H.求证OP+OM+ON=AH.
如图,AB=AC,AD=AE,BD、CE交于O,求证AO平分∠BAC.
△ABC的外角∠CBD,∠BCE的角平分线交于点F,求证AF平分∠BAC.
如图,P为∠AOB内一点,OA=OB,且△OPA与△OPB面积相等,求证∠AOP=∠BOP.