一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h 以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
如图所示,在足够长的光滑水平轨道上静止三个小木块A,B,C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失)。现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在BC之间的弹簧第一次恢复到原长时追上B,并且在碰撞后和B粘到一起。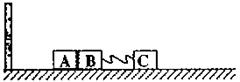
求:
(1)在A追上B之前弹簧弹性势能的最大值;
(2)A与B相碰以后弹簧弹性势能的最大值。
如图所示,有一玻璃管长L=100cm,内有一段水银柱h=20cm,封闭着长a=50cm长的空气柱,此时温度t1=27oC,大气压恒为p0=76cmHg,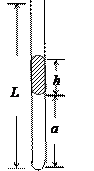
求:
(1)求当对气体加热使水银柱升到与管口平齐时,气体温度为多少?
(2)求空气柱温度至少多大时,可使管中水银全部溢出?
(8分)下列是《驾驶员守则》中的安全距离图示和部分安全距离表格.
| 车速v(km/h) |
反应距离s(m) |
刹车距离x(m) |
停车距离L(m) |
| 40 |
10 |
10 |
20 |
| 60 |
15 |
22.5 |
37.5 |
| 80 |
A=( ) |
B=( ) |
C=( ) |
请根据该图表计算:
(1)如果驾驶员的反应时间一定,请在表格中填上A的数据;
(2)如果路面情况相同,请在表格中填上B、C的数据;
(3)如果路面情况相同,一名喝了酒的驾驶员发现前面50 m处有一队学生正在横过马路,此时他的车速为72 km/h,而他的反应时间比正常时慢了0.1 s,请问他能在50 m内停下来吗?
太阳中含有大量的氘核,因氘核不断发生核反应释放大量的核能,以光和热的形式向外辐射.已知氘核质量为2.013 6 u,氦核质量为3.015 0 u,中子质量为1.008 7 u,1 u的质量相当于931.5 MeV的能量则:
(1)求核反应中释放的核能.
(2)在两氘核以相等的动能0.35 MeV进行对心碰撞,并且核能全部转化为机械能的情况下,求反应中产生的中子和氦核的动能.
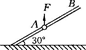
(15分)如图所示,一重为l0 N的小球,在F="20" N的竖直向上的拉力作用下,从A点由静止出发向上运动.F作用1.2 s后撤去,已知杆与球间的动摩擦因数为 ,试求从撤去力F开始计时,小球经多长时间将经过距A点2.2m的B点.(g取10 m/s2)
,试求从撤去力F开始计时,小球经多长时间将经过距A点2.2m的B点.(g取10 m/s2)