计算下列各题(每小题4分,共40分):
(1)16+(-9)
(2)7.6—(-2.7)
(3)—5+ 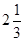
(4)(—9)+(—18)
(5)2-(-4)+8÷(-2)+(-3).
(6)(—1)2-(- )3÷4;
)3÷4;
(7)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2);
(8)-32×(-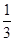 )2-(-2)3÷(-
)2-(-2)3÷(- )2
)2
(9)3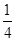 +(-2
+(-2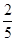 )+5
)+5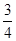 -8
-8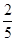 ;
;
(10)( +
+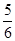 -
-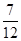 )×(-24)
)×(-24)