（本题9分）把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的式子，或可以求出一些不规则图形的面积．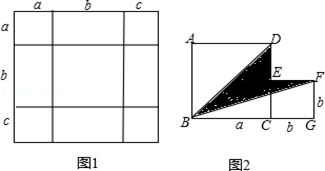
（1）如图1，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论，请用等式表示出来。
（2）如图2，是将两个边长分别为a和b的正方形拼在一起，B、C、G三点在同一直线上，连接BD和BF，若两正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积。
如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中
.
（1）操作发现(4分)
如图2，固定△ABC ，使△DEC绕点C旋转。当点D恰好落在AB边上时，填空：
线段DE与AC的位置关系是；
设△BDC的面积为
，△AEC的面积为
。则与的数量关系是。
（2）猜想论证
当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中与的数量关系仍然成立，并尝试分别作出了△BDC，△AEC中
边上的高，请你证明小明的猜想。
如图，已知：D是△ABC中BC边上一点，EB=EC，∠ABE=∠ACE，求证：∠BAE=∠CAE.
证明：在△AEB和△AEC中，
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE(第二步)
问：上面证明过程是否正确？若正确，请写出每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程；
如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC上，且BE=BD，连结AE、DE、DC.
①求证：△ABE≌△CBD；
②若∠CAE=30°，求∠BDC的度数.
如下图，CD⊥AD，CB⊥AB，AB=AD，求证：CD=CB.
如图，在△ABC中，∠ACB＝90°，BC＝15，AC＝20，CD是高．
(1)求AB的长；
(2)求△ABC的面积；
(3)求CD的长．