如图,一条公路的转弯处是一段圆弧( ).
).
(1)用直尺和圆规作出 所在圆的圆心
所在圆的圆心 ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若 的中点
的中点 到弦
到弦 的距离为
的距离为 m,
m, m,求
m,求 所在圆的半径.
所在圆的半径.
已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B,点C.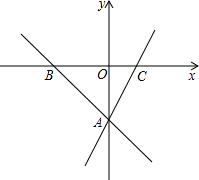
(1)求m的值及△ABC的面积;
(2)求一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标.
若一次函数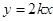 与
与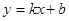 (
(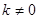 ,
,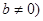 的图像相交于点
的图像相交于点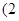 ,
,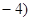 .
.
(1)求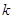 、
、 的值;
的值;
(2)若点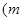 ,
,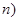 在函数
在函数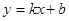 的图像上,求
的图像上,求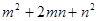 的值。
的值。
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: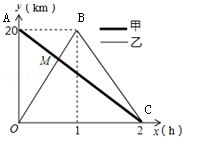
(1)直接写出甲骑自行车的速度 ;乙骑自行车的速度 ;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过2km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
一次函数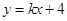 的图象经过点A(−3,−2).
的图象经过点A(−3,−2).
(1)求这个一次函数的关系式;
(2)判断点B(-5,3)是否在这个函数的图象上.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.