如图所示,电源电动势E=10V,内阻r=1Ω,闭合电键S后,标有“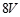 ,
,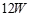 ”的灯泡恰能正常发光,电动机M绕组的电阻R0=4Ω,求:
”的灯泡恰能正常发光,电动机M绕组的电阻R0=4Ω,求: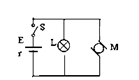
(1)电源的输出功率P0;
(2)10s内电动机产生的热量Q;
(3)电动机的效率;
(4)若用此电动机由静止开始加速提升一质量为0.5kg的物体,10s末物体的速度达到4m/s,且在这一过程中电动机输出功率保持不变,物体也不会碰到电动机,求物体在这10s内上升的高度h(忽略空气阻力和一切摩擦作用).
在均匀介质中选取平衡位置在同一直线上的9个质点,相邻两质点的距离均为 =0.3m,如图(a)所示,一列横波沿该直线向右传播,t=0时刻到达质点1,质点1开始向下运动,经过时间⊿t=0.6s第一次出现如图(b)所示的波形。求:(1)该波的周期和波速;(2)在图(c)中画出从t=0开始,质点4的振动图象(至少画出一个周期,标出必要的刻度值)。
=0.3m,如图(a)所示,一列横波沿该直线向右传播,t=0时刻到达质点1,质点1开始向下运动,经过时间⊿t=0.6s第一次出现如图(b)所示的波形。求:(1)该波的周期和波速;(2)在图(c)中画出从t=0开始,质点4的振动图象(至少画出一个周期,标出必要的刻度值)。

如图所示,一透明半圆柱体横截面半径为R,长为L,折射率为n=1.55。一平行光束从半圆柱体的矩形表面垂直射入,部分柱面有光线射出。求该部分柱面的面积。(sin π=
π=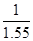 )
)
(17分)如图,在光滑的水平长轨道上,质量为m的小球P1和质量M的小球P2分别置于A、C两点,从某时刻起,P1始终受到向右的大小恒定为F的力作用而向右运动,到C点时与P2发生水平对心正碰(碰撞时间很短,可忽略不计),碰后瞬间P1速度变为零.已知AC、BC间距离分别为LAC=2L,LCB=L,M=3m.试求:
(1)碰后瞬间P2的速度大小;
(2)两球第二次碰撞前的最大距离dm .
(13分)如图所示,在沙堆表面放置一长方形木块A,其上面再放一个质量为m=0.10kg的爆竹B,木块的质量为M=6.0kg。当爆竹爆炸时,因反冲作用使木块陷入沙中深度h=5cm,而木块所受的平均阻力为f=80N。若爆竹的火药质量以及空气阻力可忽略不计,g取10m/s2,求爆竹能上升的最大高度。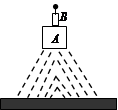
(15分)如图所示,均匀介质中两波源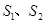 分别位于x轴上
分别位于x轴上 14m处,质点P位于x轴上
14m处,质点P位于x轴上 4m处,
4m处,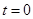 时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源
时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源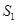
 的振幅均为A=2cm,则
的振幅均为A=2cm,则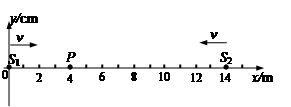
①经过多长时间,由波源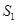 发出的波到达P点?
发出的波到达P点?
②从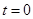 至
至 0.35s内质点P通过的路程多少?
0.35s内质点P通过的路程多少?