如图所示,某潜水员在检查装有透明液体的圆柱体容器,当潜水员的眼睛在容器中心轴位置且在液面下h2=1m处时,他看到容器口处所有景物都出现在一个顶角为60°的倒立圆锥里,已知容器口距离容器液面的距离h1=1m,圆柱体的横切面半径 。
。
①求容器中液体的折射率。
②若一个身高h3=1m的小孩站在离容器口边缘 远的位置,小孩恰好能看到对面的容器底部,则容器中液体的深度为多少米?
远的位置,小孩恰好能看到对面的容器底部,则容器中液体的深度为多少米?
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电的小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间中突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹经过A点.设小球运动过程中带电量没有改变,重力加速度为g,求: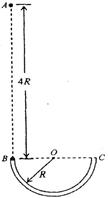
(1)小球到达B点的速度大小;
(2)小球受到的电场力的大小;
(3)小球经过管口C处时对圆管壁的压力.
如图所示,在一磁感应强度B=0.5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为h=0.1m的平行光滑的金属导轨MN与PQ,导轨的电阻忽略不计.在两根导轨的端点N、Q之间连接一阻值R=0.3Ω的电阻,导轨上跨放着一根长为L=0.2m,每米长电阻r=2.0Ω/m的金属棒ab,金属棒与导轨正交,交点为c、d.当金属棒以速度v=4.0m/s向左做匀速运动时,试求: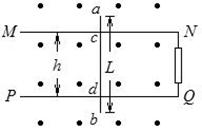
(1)电阻R中的电流强度大小和方向;
(2)使金属棒做匀速运动的外力;
(3)金属棒ab两端点间的电势差.
如图所示,起重机将重物吊运到高处的过程中经过A、B两点,重物的质量m="500" kg,A、B间的水平距离d ="10" m.重物自A点起,沿水平方向做v="1.0" m/s的匀速运动,同时沿竖直方向做初速度为零、加速度a=" 0.2" m/s2的匀加速运动,忽略吊绳的质量及空气阻力,取重力加速度g=" 10" m/s2.求: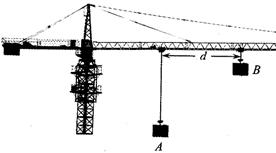
(1)定性画出重物由A到B的运动轨迹;
(2)重物由A运动到B的时间;
(3)重物经过B点时速度的大小;
(4)由A到B的过程中,吊绳对重物所做的功.
如图为一块直角三棱镜,顶角A为30°。一束激光沿平行于BC边的方向射向直角边AB,并从AC边射出,出射光线与AC边夹角也为30°。求:
① 棱镜的折射率n;
② 该激光在棱镜中的传播速度v。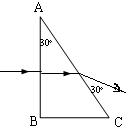
如图甲所示,两根足够长、电阻不计的光滑平行金属导轨相距为L1=1m,导轨平面与水平面成θ=30°角,上端连接阻值R=1.5Ω的电阻;质量为m=0.2kg、阻值r=0.5Ω的匀质金属棒ab放在两导轨上,距离导轨最上端为L2=4m,棒与导轨垂直并保持良好接触。整个装置处于一匀强磁场中,该匀强磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图乙所示。(g=10m/s2)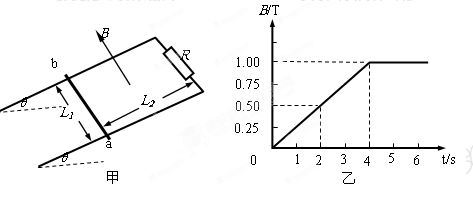
(1)保持ab棒静止,在0~4s内,通过金属棒ab的电流多大?方向如何?
(2)为了保持ab棒静止,需要在棒的中点施加了一平行于导轨平面的外力F,求当t=2s时,外力F的大小和方向;
(3)5s后,撤去外力F,金属棒将由静止开始下滑,这时用电压传感器将R两端的电压即时采集并输入计算机,在显示器显示的电压达到某一恒定值后,记下该时刻棒的位置,测出该位置与棒初始位置相距2.4m,求金属棒此时的速度及下滑到该位置的过程中在电阻R上产生的焦耳热。