古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )


| A.36 = 15+21 | B.49 = 18+31 |
| C.25 = 9+16 | D.13 = 3+10 |
已知过点(2,-3)的直线y=ax+b(a≠0)不经过第一象限,设s=a+2b,则s的取值范围是()
A.-5≤s≤-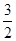 |
B.-6<s≤-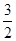 |
C.-6≤s≤-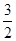 |
D.-7<s≤-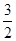 |
二次函数y=mx2+x-2m(m是非0常数)的图象与x轴的交点个数为()
| A.0个 | B.1个 | C.2个 | D.1个或2个 |
如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于()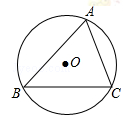
A.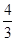 |
B.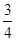 |
C.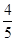 |
D.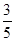 |
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为()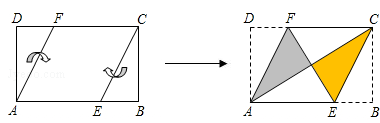
| A.1 | B.2 | C.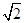 |
D.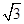 |
如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为()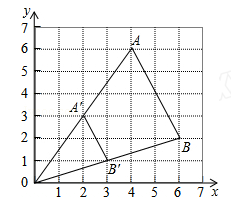
A.( ,n) B.(m,n) C.(m,
,n) B.(m,n) C.(m,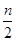 ) D.(
) D.( ,
,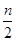 )
)