一轻质细绳一端系一质量为m=
kg的小球A，另一端挂在光滑水平轴O上，O到小球的距离为L=0.1m，小球跟水平面接触，但无相互作用，在球的两侧等距离处分别固定一个光滑的斜面和一个挡板，如图所示，水平面长s=2m，动摩擦因数为μ=0.25．现有一滑块B，质量也为m，从斜面上滑下，每次与小球碰撞时相互交换速度，且与挡板碰撞时不损失机械能．若不计空气阻力，并将滑块和小球都视为质点，g取10m/s2，（斜面底端和水平面光滑连接）．试问：
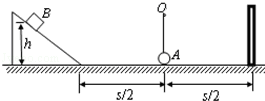
（1）若滑块B从斜面上高度h=3.2m处滑下，要保证运动过程中绳子不会断，绳子的最大承受拉力至少应为多大？
（2）若滑块B从斜面上高度h′处滑下与小球第一次碰后，使小球恰好在竖直平面内做完整的圆周运动，求此高度h′．
（3）若滑块B从H="2.8m" 处下滑与小球碰撞后，小球在竖直平面内做圆周运动，求小球做完整圆周运动的次数n．
如图所示，在x轴上方存在垂直xOy平面向外的匀强磁场，坐标原点O处有一粒子源，可向x轴和x轴上方的各个方向不断地发射速度大小均为v、质量为m、带电量为+q的同种带电粒子。在x轴上距离原点xo处垂直于x轴放置一个长度为xo、厚度不计、能接收带电粒子的薄金属板P（粒子一旦打在金属板P上，其速度立即变为0）。现观察到沿x轴负方向射出的粒子恰好打在薄金属板的上端，且速度方向与y轴平行。不计带电粒子的重力和粒子间相互作用力。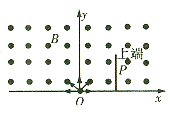
（1）求磁感应强度B的大小；
（2）求被薄金属板接收的粒子中运动的最长与最短时间的差值；
（3）若在y轴上放置一挡板，使薄金属板右侧不能接收到带电粒子，试确定挡板的最小长度和放置的位置坐标。
如图所示，一足够长的、倾角a=37°的斜面，固定在水平地面上。一质量m="l" kg的物体（视为质点）在水平恒定推力F作用下，从斜面底端由静止沿斜面向上运动，运动一段距离后立即撤去推力F，此后物体继续运动。在物体上升的阶段，每隔0．2 m通过速度传感器测得物体的瞬时速度的大小，下表给出了部分测量数据。物体与斜面间的动摩擦因数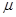
处处相同，g取l0 m/s2，sin 37°=0．6，cos 37°=0．8。求：
（1）物体与斜面间的动摩擦因数；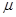
（2）推力F的大小；
（3）当物体向上运动到x="0.8" m时物体的瞬时速度大小。
如图所示，在光滑水平面上有均可视为质点的A、B、C三个弹性小球，其质量分别为mA=2m、mB=m、mC=3m，其中A、B之间用一轻弹簧相连。开始时A、B、C都处于静止状态，弹簧处于原长，且C距离B足够远，现给A一个水平向右的初速度v0．当B达最大速度时恰好与C发生弹性碰撞，求：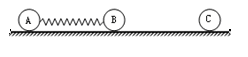
⑴B达最大速度时，Ａ和Ｂ的速度；
⑵B以最大速度与C相碰后，弹簧所具有的最大弹性势能Ep 。
如图所示，用折射率
的玻璃做成内径为
、外径为
的半球形空心球壳，一束平行光射向此半球的外表面，与中心对称轴
平行，试求：
①入射角
满足什么条件的光线可以射出内球面（不考虑多次反射）；
②如果要使球壳内表面没有光线射出，在球壳左边至少用多大的遮光板，如何放置才行？
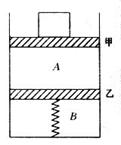
如图所示，一端封闭一端开口粗细均匀的绝热玻璃管的横截面积为10cm2，管内有两个重力不计的活塞，导热活塞甲封闭了长30cm的气柱A，绝热活塞乙用一根劲度系数
、原长为15cm的轻质弹簧和管底相连，气柱B长15cm，气体的初始温度为27℃，现在甲活塞上放一个2kg的砝码，待活塞稳定后再加热气体B，求当气体B的温度升高多少时，活塞甲可返回原处？（大气压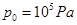
，摩擦不计，
）