如图所示的螺线管的匝数n=1500，横截面积S=20cm2，电阻r=1.5Ω，与螺线管串联的外电阻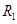
=10Ω，R2=3.5Ω。若穿过螺线管的磁场的磁感应强度按图（b）所示的规律变化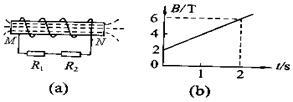
求（1）螺线管两端M、N间的电压。
（2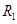）上消耗的电功率。
一质量m＝2.0 kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面，某同学利用传感器和计算机做出了小物块上滑过程的速度—时间图像如图所示．
(取sin 37°＝0.6cos 37°＝0.8，g＝10 m/s2)求：
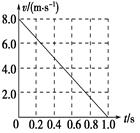
(1)小物块冲上斜面过程中加速度的大小；
(2)小物块所到达斜面最高点与斜面底端距离。
(3)小物块与斜面间的动摩擦因数。
如图所示，底座A上装有长0.5 m的直立杆，总质量为2kg，杆上套有质量为0.5kg的小环B，它与杆有摩擦，当环从底座上以4 m／s速度升起时，刚好能到达顶端．(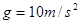
)求:
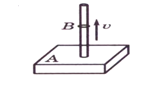
(1) 在小环升起过程中，水平面对底座支持力多大？
(2) 小环从杆顶端落回底座需多少时间?
如图所示，气球重10N，空气对其浮力竖直向上大小为16N。由于受水平风力的影响，系气球的绳子与水平面成θ= 60。角，气球保持静止。求绳子的拉力大小，水平风力大小。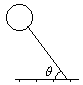
物体从静止开始做匀加速直线运动，前2s内的位移是8m，试求以下问题。
①第3s内位移。
②速度从6m / s增至10m / s发生的位移。
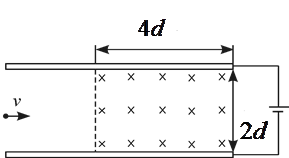
如图所示，两块水平放置、相距为
的长金属板接在电压可调的电源上。两板之间的右侧长度为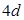
的区域存在方向垂直纸面向里的匀强磁场，磁感应强度为
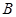。喷墨打印机的喷口可在两极板左侧上下自由移动，并且从喷口连续不断喷出质量均为
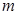、速度水平且大小相等、带等量电荷的墨滴。调节电源电压至
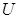，使墨滴在电场的左侧区域恰能沿水平方向向右做匀速直线运动。（重力加速度为
）
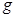（1）判断墨滴所带电荷的种类，并求其电荷量；
（2）要使墨滴不从两板间射出，求墨滴的入射速率应满足的条件。