(本小题满分12分)函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且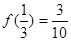 .
.
(1)求实数 ,并确定函数
,并确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值.(本小问不需说明理由)
有无最大值或最小值?如有,写出最大值或最小值.(本小问不需说明理由)
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
(理科)已知四棱锥 的底面
的底面 是直角梯形,
是直角梯形, ,
, ,
,
侧面 为正三角形,
为正三角形, ,
, .如图4所示.
.如图4所示.
(1) 证明: 平面
平面 ;
;
(2) 求四棱锥 的体积
的体积 .
.
.已知椭圆C1的方程为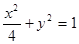 ,双曲线C2的左
,双曲线C2的左 、右焦点分别为C1的
、右焦点分别为C1的 左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线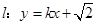 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足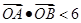 (其中O为原点),求k的取值范围。
(其中O为原点),求k的取值范围。
. 设函数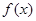 是定义在
是定义在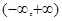 上的增函数,若不等式
上的增函数,若不等式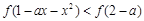 对于任意
对于任意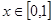 恒成立,求实数
恒成立,求实数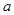 的取值范围。
的取值范围。
已知:双曲线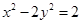 的左、右两个焦点分别为
的左、右两个焦点分别为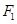 、
、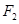 ,动点
,动点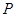 满足
满足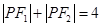 。
。
(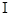 )求:动点
)求:动点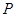 的轨迹
的轨迹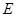 的方程;
的方程;
(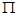 )若
)若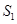 、
、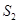 分别为(1)中曲线
分别为(1)中曲线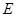 的左、右焦点,
的左、右焦点,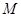 是曲线
是曲线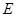 上的一个动点,
上的一个动点,
求: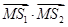 的最大值和最小值。
的最大值和最小值。
有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字,函数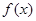 =
=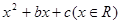 。
。
(Ⅰ)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数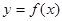 有零点的概率;
有零点的概率;
(Ⅱ) 求函数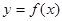 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率