(本小题满分13分)有两个投资项目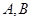 ,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)
,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)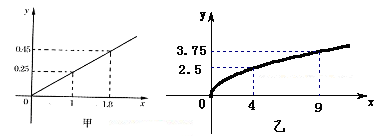
(1)分别将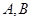 两个投资项目的利润表示为投资
两个投资项目的利润表示为投资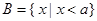 (万元)的函数关系式;
(万元)的函数关系式;
(2)现将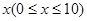 万元投资
万元投资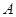 项目,
项目,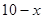 万元投资
万元投资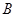 项目.
项目.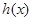 表示投资A项目所得利润与投资
表示投资A项目所得利润与投资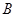 项目所得利润之和.求
项目所得利润之和.求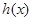 的最大值,并指出
的最大值,并指出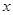 为何值时,
为何值时,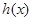 取得最大值
取得最大值
(本小题满分14分)东华旅行社为某旅游团包飞机去旅游,其中旅行社的包机费为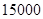 元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在
元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在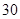 人或
人或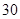 人以下,飞机票每张收费
人以下,飞机票每张收费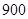 元;若旅游团的人数多于
元;若旅游团的人数多于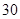 人,则给予优惠,每多
人,则给予优惠,每多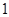 人,机票费每张减少
人,机票费每张减少 元,但旅游团的人数最多有
元,但旅游团的人数最多有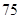 人,设旅游团的人数为
人,设旅游团的人数为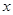 人,每张飞机票价为
人,每张飞机票价为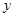 元,旅行社可获得的利润为
元,旅行社可获得的利润为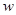 元.
元.
(1)写出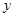 与
与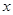 的函数关系式;
的函数关系式;
(2)写出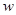 与
与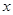 的函数关系式;
的函数关系式;
(3)那么旅游团的人数为多少时,旅行社可获得的利润最大?
(本小题满分14分)已知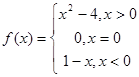
(1)求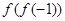 ,
,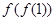 ;
;
(2)画出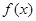 的图像;
的图像;
(3)若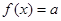 ,问
,问 为何值时,方程没有根?有一个根?两个根?
为何值时,方程没有根?有一个根?两个根?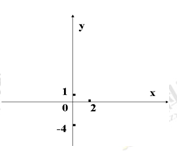
(本小题满分12分)
(1)
(2)
(本小题满分12分)已知全集 ,集合
,集合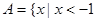 或
或 ,
,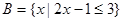 .
.
求:(1)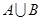 (2)
(2)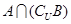 (3)
(3)  .
.
已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式.
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围.
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.