如图所示,水平放置的A.B两平行板间距h,上板A带正电,现有质量为m,电荷量为+q的小球在B板下方距离为H处,以初速度v0竖直向上从B板小孔进入板间电场,欲使小球刚好打到A板,A.B间电势差UAB应为多大?(不能忽略重力)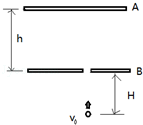
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。试推导第一宇宙速度v的表达式。
如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上。一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点。已知水平轨道AB长为L。求:
(1)小物块与水平轨道的动摩擦因数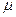
(2)为了保证小物块不从轨道的D端离开轨道,圆弧轨道的半径R至少是多大?
(3)若圆弧轨道的半径R取第(2)问计算出的最小值,增大小物块的初动能,使得小物块冲上轨道后可以达到最大高度是1.5R处,试求物块的初动能并分析物块能否停在水平轨道上。如果能,将停在何处?如果不能,将以多大速度离开水平轨道?
太阳能已经越来越广泛的被应用,为了测量太阳的辐射功率,物理兴趣小组的同学做如下的简单实验:取一个横截面积为S=3×10-2m2的不高的圆筒,筒内装有0.6kg的水,用来测量太阳的辐射到地面的能量,某一天中午在太阳光直射2min后,水的温度升高了10C,求:
(1)在阳光直射下,地球表面每平方厘米获得的能量。
(2)假设射到大气顶层的太阳能只有43%到达地面,另外57%被大气吸收和反射而未到地面,你能由此估算出太阳的功率吗?
质量为5´103 kg的汽车在t=0 时刻速度v0=10m/s,随后以P=6´104 W的额定功率沿平直公路继续前进,经72s达到最大速度,设汽车受恒定阻力,其大小为2.5´103N。求:
时刻速度v0=10m/s,随后以P=6´104 W的额定功率沿平直公路继续前进,经72s达到最大速度,设汽车受恒定阻力,其大小为2.5´103N。求:
(1)汽车的最大速度vm;
(2)汽车在72s内经过的路程s。
如图所示,是上海“明珠线”某轻轨车站的设计方案,与站台连接的轨道有一个小坡度,电车进站时要上坡,出站时要下坡.如果坡高2m,电车到a点时的速度是25.2km/h,此后便切断电动机的电源,如果不考虑电车所受的摩擦力,则电车到a点切断电源后,能否冲上站台?如果能冲上,它到达b点时的速度多大?如果不能,请说明理由.