为了研究过山车的原理，某物理小组提出了下列的设想：取一个与水平方向夹角为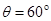
，长为
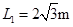的倾斜轨道AB，通过微小圆弧与长为
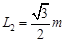的水平轨道BC相连，然后在C处设计一个竖直完整的光滑圆轨道，出口为水平轨道D，如图所示。现将一个小球从距A点高为h="0.9" m的水平台面上以一定的初速度
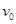水平弹出，到A点时速度方向恰沿AB方向，并沿倾斜轨道滑下。已知小球与AB和BC间的动摩擦因数均为
。
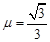取10m/s2，求：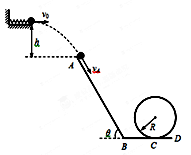
（1）小球初速度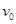的大小；
（2）小球滑过C点时的速率
；
（3）要使小球不离开轨道，则竖直圆弧轨道的半径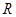
应该满足什么条件。
一列简谐波沿x轴传播，t=0时刻的波形如图，此时质点P振动方向为+y，6s后P第一次处 于波谷，求简谐波传播的速度大小和方向．
取一滴油酸酒精溶液滴到水面上，酒精溶于水，油酸在水面上形成一单分子薄膜，测出这一薄膜的面积为0．2m2，已知油酸分子的直径为5×10 －10m，1 cm3的油酸酒精溶液有50滴，试估算原油酸酒精溶液的体积浓度（
×100%）．
如图所示，A、B两小球质量分别为mA=0.05kg、mB=0.lkg，用一根长为L=1.0rn的细绳连接，细绳是不能伸长的轻绳，A球套在一根斜放的粗糙杆上，杆与水平面夹角θ=300。起始，同时给A、B一个方向沿杆向下、大小相同的初速度，此后观察到A、B连线保持竖直。当A球运动到P点时，碰到钉子突然停下，B球继续运动，但沿绳方向的速度瞬间消失，只剩下垂直绳方向的速度，B球恰好能不与杆相碰，不计空气阻力，已知OP间的竖直高度为向h= l.0m，g取10m/s2，求：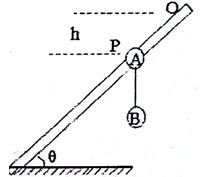
（1）A与杆接触面间的动摩擦因数μ。
（2）初速度v0的大小。
（3）整个过程中系统损失的机械能ΔE。
如图所示，半径R=0.40m的光滑半圆环轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A。质量m=0.l0kg的小球与水平地面之间的动摩擦因数为μ=0.3，小球以初速度v0="7.0" m/s在水平地面上向左运动4.0m后，冲上竖直半圆环，最后小球落在C点，取重力加速度g="10" m/s2，求：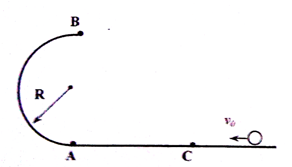
（1）小球进入圆轨道通过A点时对轨道的压力；
（2）小球经过B点时速度；
（3）A、C间的距离；
如图所示，ABC为绝缘体轨道，斜面部分倾角为30o，与下滑物体间动摩擦因数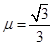
，水平轨道光滑。斜面轨道处于场强为E=l×106V/m、方向平行斜面向下的匀强电场中。小物体甲的质量m=0.1kg，带正电，电荷量为q=0.5×10-6 C，从斜面上高h="5" cm的A点由静止释放．同时小物体乙（不带电）自C点以速度v0沿水平面向左匀速运动，C点与斜面底端B处的距离L="0.4" m．甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去，甲释放后经过t="l" s刚好追上乙。取g=" 10" m/s2，求：
（1）甲沿斜面运动的加速度的大小：
（2）甲到达B点时的速率：
（3）乙的速度v0的大小。