我国于2013年12月发射了嫦娥三号卫星，该卫星在距月球表面高度为h的轨道上做匀速圆周运动，其运行的周期为T，卫星还在月球上软着陆。若以R表示月球的半径，忽略月球自转及地球对卫星的影响，则（ ）
A．月球的第一宇宙速度为 |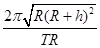
B．嫦娥三号卫星绕月运行时的向心加速度为 |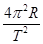
C．物体在月球表面自由下落的加速度大小为 |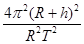
| D．由于月球表面是真空，嫦娥三号降落月球时，无法使用降落伞减速 |
处在磁场中的一闭合线圈，若没有产生感应电流，则可以判定（）
| A．线圈没有在磁场中运动 |
| B．线圈没有做切割磁感线运动 |
| C．磁场没有发生变化 |
| D．穿过线圈的磁通量没有发生变化 |
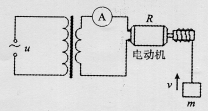
．如图所示为一理想变压器，原、副线圈的匝数比为n，原线圈接电压为u=U0sinωt的正弦交流电，输出端接有一个交流电流表和一个电动机，电动机的线圈电阻为R．当输入端接通电源后，电动机带动一质量为m的重物匀速上升，此时电流表的
示数为I，重力加速度为g，下列说法正确的是（）
| A．电动机两端电压为IR |
| B．原线圈中的电流为nI |
C．电动机消耗的电功率为 |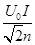
D．重物匀速上升的速度为 |
飞机水平匀速飞行，从飞机上每隔ls释放一个小球，先后共释放A、B、C、D四个小球，不计空气阻力，则四个球（）
A．在空中运动时，4个小球排成一条竖直线
B．小球D刚离飞机时，A、B两小球的间距为25m
C．空中运动时，A球速度大小始终比B球大10m/s
D．四个小球的落地点间隔越来越大
如图所示，在一个粗糙的绝缘水平面上，彼此靠近地放置两个带正电荷的小物块。由静止释放后，两个物块向相反方向运动，并最终停止．在物块的运动过程中，下列表述正确的是（）
| A．物块受到的摩擦力始终小于其受到的库仑力 |
| B．物块先作匀加速直线运动，再作匀减速运动 |
| C．因摩擦力始终做负功，故两物块组成的系统的机械能一直减少 |
| D．整个过程中物块受到的库仑力做的功等于电势能的减少 |
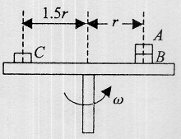
如图叠放在水平转台上的小物体A、B、C能随转台一起以角速度ω匀速转动，A、B、C的质量分别为3m、2m、m，A与B、B与转台、C与转台间的动摩擦因数都为μ，B、C离转台中心的距离分别为r、1.5r，设本题中的最大静摩擦力等于滑动摩擦力，以下说法正确的是（）
A．B对A的摩擦力一定为3μmg
B．C与转台间的摩擦力大于A与B间的摩擦力
C．转台的角速度一定满足：
D．转台的角速度一定满足：
