如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A、点Q从顶点B同时出发,且它们的速度都为1cm/s,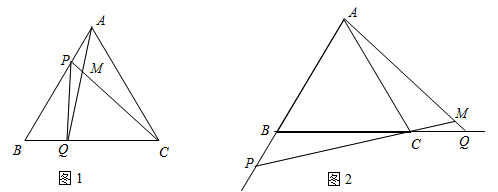
(1)连接AQ、CP交于点M,则在点P、Q运动过程中,∠CMQ变化吗?若变化,则说明理由;若不变,则求出它的度数。
(2)求何时△PBQ是直角三角形?
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,说明理由;若不变,求出它的度数。
如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12 ,点C的坐标为(-18,0)。
,点C的坐标为(-18,0)。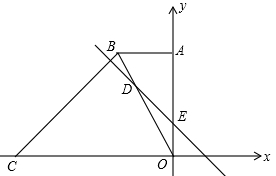
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式;
(3)若点P是(2)中直线DE上的一个动点,在坐标平面内是否存在点Q,使以O、E、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。
国务院总理温家宝2011年11月16日主持召开国务院常务会议,会议决定建立青海三江源国家生态保护综合实验区。现要把228吨物资从某地运往青海甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资。已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
| 运往地 车 型 |
甲 地(元/辆) |
乙 地(元/辆) |
| 大货车 |
720 |
800 |
| 小货车 |
500 |
650 |
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费。
在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF。
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变, 如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明。
甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度) 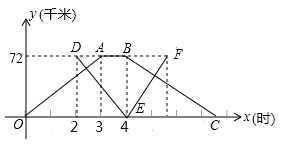
(1)轮船在静水中的速度是千米/时;快艇在静水中的速度是千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
最美女教师张丽莉在危急关头为挽救两个学生的生命而失去双腿,她的病情牵动了全国人民的心,全社会积极为丽莉老师献爱心捐款。为了解某学校的捐款情况,对学校捐款学生进行了抽样调查,把调查结果制成了下面两个统计图,在条形图中,从左到右依次为A组、B组、C组、D组、E组,A组和B组的人数比是5:7。捐款钱数均为整数,请结合图中数据回答下列问题: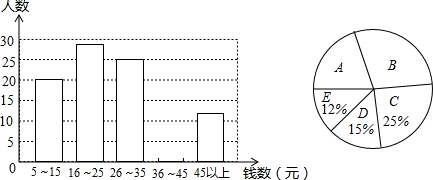
(1)B组的人数是多少?本次调查的样本容量是多少?
(2)补全条形图中的空缺部分,并指出中位数落在哪一组?
(3)若该校3000名学生都参加了捐款活动,估计捐款钱数不少于26元的学生有多少人?