(本小题满分10分)如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形 .解答下列问题:
.解答下列问题: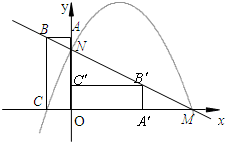
(1)求出直线 的函数解析式;
的函数解析式;
(2)直线 与
与 轴交于点M、与y轴交于点N,抛物线
轴交于点M、与y轴交于点N,抛物线 的图象经过点C、M、N,求抛物线的函数解析式;
的图象经过点C、M、N,求抛物线的函数解析式;
(3)将△MON沿直线MN翻折,点O落在点P处,请你判断点P是否在抛物线上,说明理由.
解不等式组
解不等式组: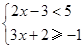
某“希望学校”为加强信息技术课教学,拟投资建一个初级计算机房和一个高级计算机房,每个机房只配置1台教师用机,若干台学生用机.现有厂方提供的产品推介单一份,如下表.
产品推介单
| 类别 |
初级机房 |
高级机房 |
| 机型 |
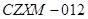 型 型 |
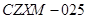 型 型 |
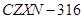 型 型 |
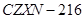 型 型 |
|
| 生产 日期 |
2005年1月 |
2005年3月 |
| 单 价 |
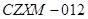 型 型10000元 |
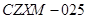 型 型14375元 |
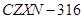 型 型4375元 |
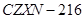 型 型8750元 |
|
| 性能 |
多人交互 |
 |
 |
 |
 |
现知:教师配置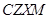 系列机型,学生配置
系列机型,学生配置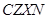 系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
请计算,拟建的两个机房各能配置多少台学生用机?
解不等式组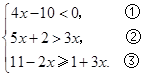
为美化青岛,创建文明城市,园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配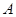 、
、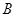 两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉情况如右表所示:
两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉情况如右表所示: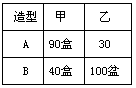
结合上述信息,解答下列问题:
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个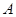 种造型的成本为1000元,搭配一个
种造型的成本为1000元,搭配一个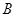 种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?
种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?