（本题9分） 某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．因受库存的影响，每批次进货个数不得超过180个，商店若将准备获利2000元，则应进货多少个？定价为多少元？
5分）八（2）班组织了一次环保知识竞赛，甲乙两队各5人的成绩如下表所示（10分制）．
| 甲 |
9 |
8 |
10 |
6 |
9 |
| 乙 |
8 |
7 |
8 |
9 |
10 |
（1）指出甲队成绩的中位数；
（2）指出乙队成绩的众数；
（3）若计算出方差为：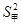
=1．84，
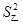=1．04，判断哪队的成绩更整齐？
如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A、C分别在x，y轴的正半轴上．点Q在对角线OB上，且QO=OC，连接CQ并延长CQ交边AB于点P．则点P的坐标为．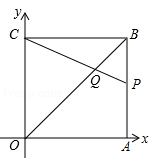
已知：如图，E是BC上一点，AB=EC，AB∥CD，BC=CD．求证：AC=ED．
如图所示，已知a∥b，AD⊥直线a，求∠A的度数．
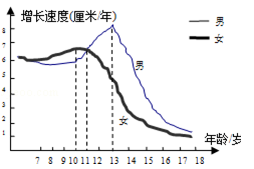
生物学研究表明，在8﹣﹣17岁期间，男女生身高增长速度规律呈现如下图所示，请你观察此图，回答下列问题，男生身高增长速度的巅峰是几岁？在几岁时男生、女生的身高增长速度是一样的？