已知抛物线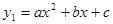
的顶点坐标为（
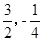）且经过点A（1，0），直线
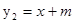恰好也经过点A
（1）分别求抛物线和直线的解析式
（2）当x取何值时，函数值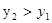
（3）当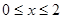
时，直接写出
的最小值分别为多少？
某商场销售一种进价为20元/台的台灯，经调查发现，该台灯每天的销售量W（台），销售单价x（元）满足W=-2x+80，设销售这种台灯每天的利润为y（元）．求y与x之间的函数关系式.
如图，放置在水平桌面上的台灯的灯臂AB长为40cm，灯罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠BAD=60°．使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？（结果精确到0.1cm，参考数据：
≈1.732）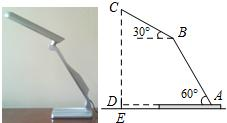
如图经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种可能性大小相同，现有两辆汽车经过这个十字路口．
（1）试用树状图或列表法中的一种列举出这两辆汽行驶方向所有可能的结果；
（2）求至少有一辆汽车向左转的概率．
我市某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图（不完整）．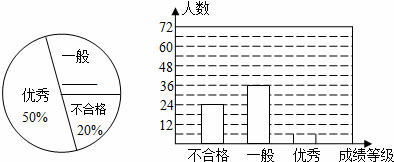
请你根据图中所给的信息解答下列问题：
（1）请将以上两幅统计图补充完整；
（2）若“一般”和“优秀”均被视为达标成绩，则该校被抽取的学生中有人达标；
（3）若该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人？
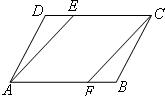
如图，在平行四边形ABCD中，BF=DE．求证：四边形AFCE是平行四边形．