乐乐和欢欢同学同时去上学，从家到学校的距离都是2km，他们走路的速度为6km/h，跑步的速度为10km/h．请根据以上信息，提出一个可以用一元一次不等式解决的问题，并给出解决办法．
如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为（0，2），D为⊙C在第一象限内的一点且∠ODB=60°，解答下列各题：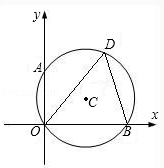
（1）求线段AB的长及⊙C的半径；
（2）求B点坐标及圆心C的坐标．
如图所示，在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC，AB分别交于点D，E，且∠CBD=∠A．判断直线BD与⊙O的位置关系，并证明你的结论．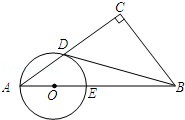
如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D．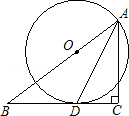
（1）求证：BC是⊙O切线；
（2）若BD=5，DC=3，求AC的长．
如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上．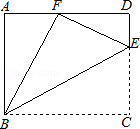
（1）求证：△ABF∽△DFE；
（2）若sin∠DFE=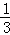
，求tan∠EBC的值．
已知抛物线y=x2﹣2x﹣8．
（1）试说明该抛物线与x轴一定有两个交点．
（2）若该抛物线与x轴的两个交点分别为A、B（A在B的左边），且它的顶点为P，求△ABP的面积．