一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
一个不透明的口袋中有三个小球,上面分别标有数字0,1,2,每个小球除数字不同外其余均相同,小华先从口袋中随机摸出一个小球,记下数字后放回并搅匀;再从口袋中随机摸出一个小球记下数字、用画树状图(或列表)的方法,求小华两次摸出的小球上的数字之和是3的概率.
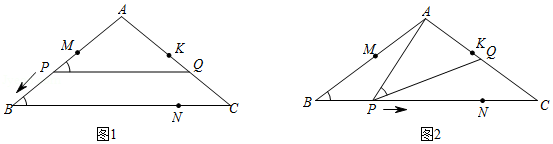
如图1和图2,在 中, , , .点 在 边上,点 , 分别在 , 上,且 .点 从点 出发沿折线 匀速移动,到达点 时停止;而点 在 边上随 移动,且始终保持 .
(1)当点 在 上时,求点 与点 的最短距离;
(2)若点 在 上,且 将 的面积分成上下 两部分时,求 的长;
(3)设点 移动的路程为 ,当 及 时,分别求点 到直线 的距离(用含 的式子表示);
(4)在点 处设计并安装一扫描器,按定角 扫描 区域(含边界),扫描器随点 从 到 再到 共用时36秒.若 ,请直接写出点 被扫描到的总时长.
如图,甲、乙两人(看成点)分别在数轴 和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率 ;
(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对 次,且他最终停留的位置对应的数为 ,试用含 的代数式表示 ,并求该位置距离原点 最近时 的值;
(3)从如图的位置开始,若进行了 次移动游戏后,甲与乙的位置相距2个单位,直接写出 的值.

表格中的两组对应值满足一次函数 ,现画出了它的图象为直线 ,如图.而某同学为观察 , 对图象的影响,将上面函数中的 与 交换位置后得另一个一次函数,设其图象为直线 .
|
|
|
0 |
|
|
|
1 |
(1)求直线 的解析式;
(2)请在图上画出直线 (不要求列表计算),并求直线 被直线 和 轴所截线段的长;
(3)设直线 与直线 , 及 轴有三个不同的交点,且其中两点关于第三点对称,直接写出 的值.

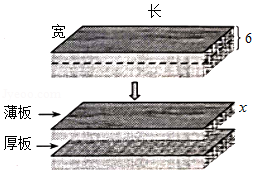
用承重指数 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数 与木板厚度 (厘米)的平方成正比,当 时, .
(1)求 与 的函数关系式.
(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为 (厘米), .
①求 与 的函数关系式;
② 为何值时, 是 的3倍? 注:(1)及(2)中的①不必写 的取值范围