设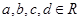 ,则“
,则“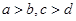 ”是“
”是“ ”成立的 ()
”成立的 ()
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设集合M= ,N=
,N= ,若
,若 ,
,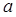 的取值范围是 ()
的取值范围是 ()
A.(− ,1) ,1) |
B.(−∞,1] | C.[1,+∞) | D.(2,+∞) |
已知 是虚数单位,复数z满足:
是虚数单位,复数z满足: ,则
,则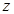 的值是()
的值是()
A. |
B. |
C.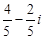 |
D. |
正四面体ABCD,线段AB 平面
平面 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面 上的射影所成角余弦值的范围是( )
上的射影所成角余弦值的范围是( )
A.[0, ] ] |
B.[ ,1] ,1] |
C.[ ,1] ,1] |
D.[ , , ] ] |
在△ABC中,已知 ,
,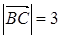 ,M、N分别是BC边上的三等分点,则
,M、N分别是BC边上的三等分点,则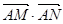 的值是( )
的值是( )
| A.5 | B. |
C.6 | D.8 |