设l、m、n表示不同的直线,α、β、γ表示不同的平面,给出下列4个命题:
①若m∥l,且m⊥α,则l⊥α;
②若m∥l,且m∥α,则l∥α;
③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;
④若α∩β=m,β∩γ=l,α∩γ=n,且n∥β,则m∥l.
其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
三个数成等差数列,其公差为d,如果最小数的2倍,最大数加7,则三个数成等比数列,且它们的积为1000,此时d为
| A.8 | B.8或-15 | C.±8 | D.±15 |
下列函数中值域是(0,+∞)的函数是
A.y=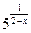 |
B.y=(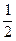 )1-x )1-x |
C.y=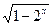 |
D.y=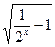 |
设O、A、B、C为平面上四个点,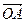 =a,
=a, =b,
=b, =c,且a+b+c=0,a,b,c两两数量积都为-1,则|a|+|b|+|c|等于
=c,且a+b+c=0,a,b,c两两数量积都为-1,则|a|+|b|+|c|等于
A.2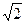 |
B.2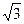 |
C.3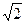 |
D.3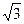 |
奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为
设I为全集,M、N、P都是它的子集,则图中阴影部分表示的集合是
| A.M∩(N∪P) | B.M∩[( IN)∩P] IN)∩P] |
C.[( IM)∩( IM)∩( IN)]∩P IN)]∩P |
D.(M∩N)∪(M∩P) |