(.河南省,第17题,9分)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.

(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
某市对电话费作了调整,原市话费为每3分钟0.2元(不足3分钟,按3分钟计算),调整后,前3分钟为0.2元,以后每分钟加收0.1元(不足1分钟按1分钟计算).
(1)根据提供的信息,完成下列表格:
| 通话时间 |
4 |
4.2 |
5.8 |
6.3 |
7.1 |
11 |
| 调整前的 话费(元) |
||||||
| 调整后的 话费(元) |
(2)若通话时间为11分钟,请你设计两种通话方案(可以分几次拨打),使所需话费小于调整后的话费.
王丽的父亲上月从工作单位取得当月工资1200元,按照个人所得税法规定,每月的个人收入超过800元的部分要纳税,超过部分不满500元的,应按照5%的税率征收个人所得税,请你思考下面的问题:
(1)王丽的父亲该月应缴纳个人所得税多少元?
(2)如果杨洁的父亲上个月缴纳个人所得税是25元,王丽的父亲与杨洁的父亲比较,哪个人的工资高?杨洁的父亲上月的工资是多少?
计算: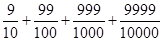
如图,用火柴棒按如图的方式搭三角表,搭一个三角形需3根火柴棒,如图甲,搭两个三角形需5根火柴棒,如图乙,搭三个三角形需7根火柴棒,如图丙,那么按此规律搭下去,搭10个三角形需要多少根火柴棒()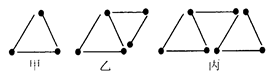
| A.30 | B.21 | C.119 | D.111 |
假日公司的西湖一日游价格如下:
A种:成人每位160元,儿童每位40元
B种:5人以上团体,每位100元
现有三对夫妇各带1个小孩,共9人,参加西湖一日游,最少要多少钱?