图中B为电源，电动势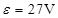
，内阻不计。固定电阻
，
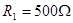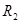为光敏电a阻。C为平行板电容器，虚线到两极板距离相等，极板长
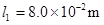，两极板的间距
，S为屏，与极板垂直，到极板的距离
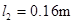。P为一圆盘，由形状相同透光率不同的三个扇形
、
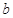和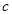
构成，它可绕
轴转动。当细光束通过、、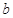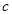照射光敏电阻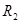时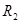，的阻值分别为1000Ω，2000Ω，4500Ω。有一细电子束沿图中虚线以速度
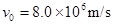连续不断地射入C。已知电子电量
，电子质量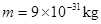
。忽略细光束的宽度、电容器的充电放电时间及电子所受重力。假设照在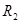上的光强发生变化时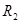阻值立即有相应的改变。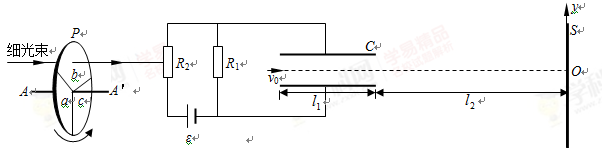
（1）设圆盘不转动，细光束通过b照射到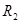上，求电子到达屏S上时，它离O点的距离y。（计算结果保留二位有效数字）。
（2）设转盘按图中箭头方向匀速转动，每3秒转一圈。取光束照在、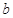分界处时
,试在答卷给出的坐标纸上，画出电子到达屏S上时，它离O点的距离y随时间t的变化图线（0~6s间）。（不要求写出计算过程，只按画出的图线评分。）
用200 N的拉力将地面上一个质量为10 kg的物体从静止开始提起5m，空气阻力不计，g取10m/s2；求：
（1）拉力的平均功率。
（2）物体提高后增加的重力势能。
（3）物体提高后具有的动能。
随着现代科学技术的飞速发展，广寒宫中的嫦娥不再寂寞，古老的月球即将留下中华儿女的足迹。航天飞机将作为能往返于地球与太空、可以重复使用的太空飞行器，备受人们的喜爱。宇航员现欲乘航天飞机对在距月球表面高h处的圆轨道上运行的月球卫星进行维修。已知月球半径为R，月球表面的重力加速度为g，万有引力常量为G。试根据以上信息求：
（1）月球的质量；
（2）维修卫星时航天飞机绕月球运行的周期。
一辆质量为2.0×103kg的汽车以恒定牵引力在水平公路上行驶，所受阻力为车重的0.2倍。其启动图像如图，已知t1=4s,此时速度v1=12m/s,t2=12s时，速度达到最大值Vm,求：
（1）汽车前4秒的加速度为多大
（2）汽车的最大速度为多大
（3）汽车加速到最大速度时位移为多大。
如图所示，一可视为质点的物体质量为m＝1 kg，在左侧平台上水平抛出，在A点速度方向恰好沿圆弧切线方向，且无能量损失进入光滑竖直圆弧轨道，并沿轨道下滑。A、B为圆弧两端点，其连线水平，O为轨道的最低点，已知圆弧半径为R＝1.0 m，对应圆心角为θ＝106°，平台与AB连线的高度差为h＝0.8 m。(重力加速度g＝10 m/s2，sin53°＝0.8，cos53°＝0.6)求：
(1)物体做平抛运动的初速度
(2)物体运动到圆弧轨道最低点O时对轨道的压力。
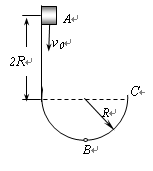
如图所示，质量为m的物体，以某一初速度从A点向下沿光滑半圆轨道运动。轨道半径为R，若物体通过B点时的速率为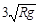
，不计空气阻力，求：
（1）物体在B点时对轨道的压力为多大
（2）物体在A点时的速度
（3）物体离开C点后还能上升多高。