先化简,再求值:(a−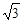 )(a+
)(a+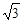 )+a(a−6),其中a=
)+a(a−6),其中a=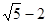 .
.
如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从C出发沿着CB方向以1cm/S的速度运动,另一动点Q从A出发沿着AC方向以2cm/S的速度运动,P、Q两点同时出发,运动时间为t(s)。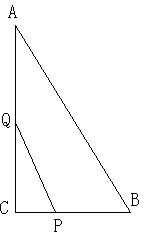
(1)当t为几秒时,△PCQ的面积是△ABC面积的 ?
?
(2)△PCQ的面积能否为△ABC面积的一半?若能,求出t的值,若不能,说明理由。
如图:在Rt△ACB中,∠C= 90°,AC=6cm,BC=8cm,点Q、 P、同时由A、B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1m/s,几秒后△PCQ 的面积为 Rt△ACB面积的一半?
某商店经销一种销售成本为每千克40元的水产品;据市场分析,若按每千克50元销售,一个月能售出500千克,销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请你回答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润.
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)设销售单价为每千克x元,月销售利润y元,求y与x的函数表达式.
某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现提高售出价,减少进货量的办法增加利润.已知这种商品每件提高1元,其销售量就要减少10件,那么他将售出价定为多少元时,才能使每天所赚利润为360元?
已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.