在平面直角坐标系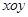 中,点
中,点 是椭圆
是椭圆 上的点,以
上的点,以 为圆心的圆与
为圆心的圆与 轴相切于椭圆的焦点F,圆
轴相切于椭圆的焦点F,圆 与
与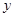 轴相交于
轴相交于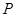 、
、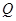 两点.若
两点.若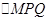 为锐角三角形,则该椭圆离心率的取值范围是 .
为锐角三角形,则该椭圆离心率的取值范围是 .
某人一周晚上值班2次,在已知他周日一定值班的条件下,他在周六晚上值班的概率为________.
[2014·洛阳统考]如图所示,矩形ABCD内的阴影部分是由曲线f(x)=2x2-2x及直线y=2x围成的,现向矩形ABCD内随机投掷一点,则该点落在阴影部分的概率为________.
某公共汽车站每隔10分钟有一辆汽车到达,乘客到达车站的时刻是任意的,则一个乘客候车时间不超过7分钟的概率是________.
[2013·江苏高考]现有某类病毒记作XmYn,其中正整数m,n(m≤7,n≤9)可以任意选取,则m,n都取到奇数的概率为________.
[2012·上海高考]三位同学参加跳高、跳远、铅球项目的比赛.若每人都选择其中两个项目,则有且仅有两人选择的项目完全相同的概率是________(结果用最简分数表示).