在长约1.0m的一端封闭的玻璃管中注满清水,水中放一个适当的圆柱形的红蜡块,将玻璃管的开口端用胶塞塞紧,并迅速竖直倒置,红蜡块就沿玻璃管由管口匀速上升到管底。将此玻璃管倒置安装在小车上,并将小车置于水平导轨上。若小车一端连接细线绕过定滑轮悬挂小物体,小车从A位置由静止开始运动,同时红蜡块沿玻璃管匀速上升。经过一段时间后,小车运动到虚线表示的B位置,如图所示。按照图3建立坐标系,在这一过程中红蜡块实际运动的轨迹可能是图中的

如图光滑水平面上有质量相等的A和B两个物体,B上装有一轻质弹簧,B原来静止,A以速度v正对B滑行,当弹簧压缩到最短时,有:()
| A.A的动量减小到最小,但不为零 |
| B.A和B具有相同的速度 |
| C.此时B的加速度达到最小 |
| D.此时A和B的总动能达到最大 |
如图所示,在光滑水平面上有一质量为M的木块,木块与轻弹簧水平相连,弹簧的另一端连在竖直墙上,木块处于静止状态,一质量为m的子弹以水平速度v0击中木块,并嵌在其中,木块压缩弹簧后在水平面做往复运动。木块自被子弹击中前到第一次回到原来位置的过程中,木块受到的合外力的冲量大小为
A B.2Mv0C.
B.2Mv0C.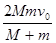 D.2mv0
D.2mv0
篮球运动员接传来的篮球时,通常要先 伸出两臂迎接,手接触到球后,两臂随球迅速引至胸前.这样做可以()
| A.减小球对手的冲量 |
| B.减小球的动量变化率 |
| C.减小球的动量变化量 |
| D.减小球的动能变化量 |
下列有关带电粒子运动的说法中 正确的是(不考虑重力)
| A.沿着电场线方向飞入匀强电场,动能、速度都变化 |
| B.沿着磁感线方向飞 入匀强磁场,动能、速 度都不变 |
| C.垂直于磁感线方向飞入匀强磁场,动能、速度都变化 |
| D.垂直于磁感线方向飞入匀强磁场,速度不变,动能改变 |
氢原子能级图的一部分如图所示,a、b、c分别表示氢原子在不同能级之间的三种跃迁途径,设在a、b、c三种跃迁过程中,放出光子的能量和波长分别是Ea、Eb、Ec和λa、λb、λc,则关系正确的是
| A.λb=λa+λc | B.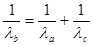 |
C.λb=λa·λc | D.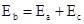 |