设数列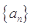 的前n项和为
的前n项和为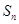 ,且
,且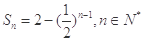 。
。
(Ⅰ)求数列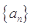 的通项公式;
的通项公式;
(Ⅱ)设数列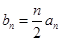 求数列
求数列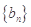 的前n项和
的前n项和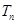 ;
;
选修 :几何证明选讲
:几何证明选讲
如图, 是圆
是圆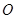 的直径,弦
的直径,弦 于
于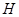 ,过
,过 延长线上一点
延长线上一点 作圆
作圆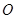 的切线交
的切线交 的延长线于点
的延长线于点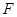 ,切点为
,切点为 ,连接
,连接 交
交 于
于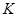 ,连接
,连接 ,且
,且

(Ⅰ)求证:
(Ⅱ)求证: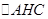 ∽
∽ .
.
已知二次函数 在
在 处的切线斜率为
处的切线斜率为 ,且
,且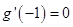 ,
, .设
.设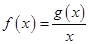 .
.
(1)若曲线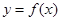 上的点
上的点 到点
到点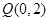 的距离的最小值为
的距离的最小值为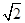 ,求
,求 的值;
的值;
(2)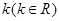 如何取值时,函数
如何取值时,函数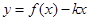 存在零点,并求出零点.
存在零点,并求出零点.
如图,在多面体 中,四边形
中,四边形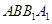 是平行四边形,
是平行四边形, ,
,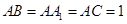 ,若
,若 是等边三角形,且
是等边三角形,且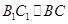 ,
,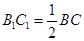 .
.
(Ⅰ)求证: 面
面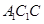 ;
;
(Ⅱ)求三棱锥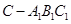 的体积.
的体积.
2014年11月10日APEC会议在北京召开,某服务部需从大学生中招收志愿者,被招收的志愿者需参加分笔试和面试两部分,把参加笔试的 40 名大学生的成绩分组: 第 1 组[75,80),第 2 组 [80,85),第 3 组[85, 90),第 4 组 [90, 95),第 5 组[95,100),得到频率分布直方图如图所示: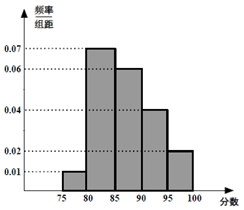
(Ⅰ)分别求成绩在第4,5组的人数;
(Ⅱ)现决定在笔试成绩较高的第 3,4,5 组中用分层抽样抽取 6 名进入面试,
①已知甲的成绩均在第4组,求甲进入面试的概率;
②若从这6名学生中随机抽取2名学生接受考官D的面试,设第3组中有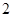 名学生被考官D面试的概率.
名学生被考官D面试的概率.
设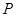 是圆
是圆 上的点,过
上的点,过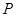 作直线
作直线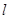 垂直
垂直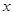 轴于点
轴于点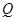 ,
,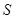 为
为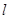 上一点,且
上一点,且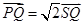 ,当点
,当点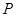 在圆上运动时,记点
在圆上运动时,记点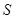 的轨迹为曲线
的轨迹为曲线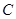 .
.
(Ⅰ)求曲线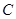 的方程;
的方程;
(Ⅱ)设动点 满足
满足 ,其中
,其中 是曲线
是曲线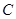 上的点,
上的点, 为原点,直线
为原点,直线 与
与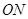 的斜率之积为
的斜率之积为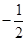 ,求证:
,求证: 为定值.
为定值.