(本题6分)如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题: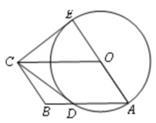
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
如图,四边形 中,
中, ∥
∥ ,点
,点 在
在 的延长线上,联结
的延长线上,联结 ,交
,交 于点
于点 ,联结
,联结 ,
, ,且
,且 .
.
(1) 求证: ;
;
(2)当 平分
平分 时,求证:四边形
时,求证:四边形 是菱形.
是菱形.
下面提供上海楼市近期的两幅业务图:图(甲)所示为2011年6月至12月上海商品房平均成交价格的走势图(单位:万元/平方米);图(乙)所示为2011年12月上海商品房成交价格段比例分布图(其中 为每平方米商品房成交价格,单位:万元/平方米).
为每平方米商品房成交价格,单位:万元/平方米).
(1)根据图(甲),写出2011年6月至2011年12月上海商品房平均成交价格的中位数;
(2)根据图(乙),可知x=;
(3)2011年12月从上海市的内环线以内、内中环之间、中外环之间和外环线以外等四个区域中的每个区域的在售楼盘中随机抽出两个进行分析:共有可售商品房2400套,其中成交200套.请估计12月份在全市所有的60000套可售商品房中已成交的并且每平方米价格低于2万元的商品房的套数.
已知:如图,在△ 中,
中, ⊥
⊥ ,
, ,
, ,
, ,求
,求 的长和
的长和 的值.
的值.
解方程组:
先化简,再求值: ,其中
,其中 .
.