己知圆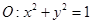 和直线
和直线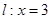 ,在
,在 轴上有一点
轴上有一点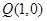 ,在圆
,在圆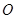 上有不与
上有不与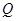 重合的两动点
重合的两动点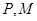 ,设直线
,设直线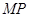 斜率为
斜率为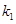 ,直线
,直线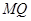 斜率为
斜率为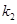 ,直线
,直线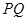 斜率为
斜率为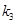 ,
,
(l)若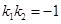
①求出 点坐标;
点坐标;
②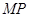 交
交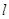 于
于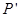 ,
,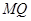 交
交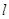 于
于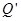 ,求证:以
,求证:以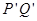 为直径的圆,总过定点,并求出定点坐标.
为直径的圆,总过定点,并求出定点坐标.
(2)若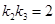 :判断直线
:判断直线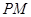 是否经过定点,若有,求出来,若没有,请说明理由.
是否经过定点,若有,求出来,若没有,请说明理由.
已知幂函数 在
在 上单调递增,函数
上单调递增,函数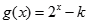 .
.
(1)求 的值;
的值;
(2)当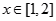 时,记
时,记 ,
,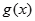 的值域分别为集合
的值域分别为集合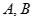 ,若
,若 ,求实数
,求实数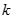 的取值范围.
的取值范围.
已知函数 .
.
(1)求函数f(x)的单调增区间.
(2)对任意 ,使得f(1)是函数f(x)在区间
,使得f(1)是函数f(x)在区间 上的最大值,求实数b的取值范围.
上的最大值,求实数b的取值范围.
已知椭圆E: 的离心率
的离心率 ,并且经过定点
,并且经过定点
(1)求椭圆E的方程;
(2)问是否存在直线y=-x+m,使直线与椭圆交于A,B两点,满足 ,若存在求m值,若不存在说明理由.
,若存在求m值,若不存在说明理由.
一个多面体的直观图及三视图如图所示,其中M ,N 分别是AF、BC 的中点

(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
在某大学自主招生考试中,所有选报II类志向的考生全部参加了数学与语文两个科目的考试,成绩分为A,B,C,D,E五个等级,某考场考生的两科考试成绩的数据统计如下图,已知该考场中数学科目成绩为B的考生有10人.
(1)求该考场考生中语文科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生数学科目平均分;
(3)已知本考场考生中,恰有2人的两科成绩均为A,在至少一科成绩为A的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为A的概率.