如下图所示,两平行金属板A、B长为L=8 cm,两板间距离d=8 cm,A板比B板电势高300 V,一带正电的粒子电荷量为q=1.0×10-10C,质量为m=1.0×10-20 kg,沿电场中心线RO垂直电场线飞入电场,初速度v0=2.0×106 m/s,粒子飞出电场后经过界面MN、PS间的无电场区域,然后进入固定在O点的点电荷Q形成的电场区域(设界面PS右侧点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为12 cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9 cm,粒子穿过界面PS做匀速圆周运动,最后垂直打在放置于中心线上的荧光屏bc上.(静电力常量k=9.0×109 N·m2/C2,粒子的重力不计)求: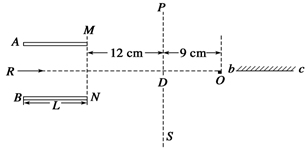
(1)粒子穿过界面MN时偏离中心线RO的距离多远?到达PS界面时离D点多远?
(2)垂直打在放置于中心线上的荧光屏的位置离D点多远?
(3)确定点电荷Q的电性并求其电荷量的大小.
分如图,将一质量为m,电荷量为+q的小球固定在绝缘杆的一端,杆的另一端可绕通过O点的固定轴转动.杆长为L,杆的质量忽略不计.杆和小球置于水平向右的匀强电场中.小球静止在A点时,绝缘杆偏离竖直方向 角.已知重力加速度为g.
角.已知重力加速度为g.
(1) 求电场强度的大小;
(2) 将杆拉至水平位置OB,在此处将小球自由释放,.求小球的最大速度的大小以及此时杆对小球的拉力.
分如图所示的电路中,直流发电机M的电动势E="250" V,内阻r =0.5Ω,R1 =R2 =1Ω.电热器组中装有50只完全相同的电热器,每只电热器的额定电压为200 V,额定功率为l 000 W,其他电阻不计,也不计电热器电阻随温度的变化.问:
(1)当接通几只电热器时,实际使用的电热器都能正常工作?
(2)当接通几只电热器时,被接通电热器的总消耗功率最大?
(3)当被接通电热器的总消耗功率最大时,电阻R1、R2和内阻r上消耗的功率分别为多少?
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行. a、b为轨道直径的两端,该直径与电场方向平行. 一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Fa和Fb,不计重力,求:
(1)电场强度的大小E;
(2)质点经过a点和b点时的动能.
如图所示,充电后的平行板电容器水平放置,电容为C,极板间的距离为d,上板正中有一小孔。质量为m、电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g).求:
(1)小球到达小孔处的速度;
(2)极板间电场强度的大小和电容器所带电荷量;
(3)小球从开始下落运动到下极板处的时间.
如图所示,在两条平行的虚线内存在着宽度为L、电场强度为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求: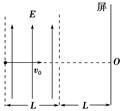
(1)粒子从射入到打到屏上所用的时间;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tan α;
(3)粒子打到屏上的点P到O点的距离x.