AB是一条平直公路上的两块路牌，一辆汽车由右向左经过B路牌时，一只小鸟恰自A路牌向B飞去，小鸟飞到汽车正上方立即折返，以原速率飞回A，过一段时间后，汽车也行驶到A．小鸟往返所用时间为t1，汽车由B路牌到A路牌所用时间为t2，且t2=2t1，小鸟和汽车运动时速率均不变，可知（ ）
A．小鸟的速率是汽车的两倍
B．相遇时小鸟与汽车位移的大小之比是3：1
C．小鸟飞行的总路程是汽车的3倍
D．小鸟和汽车在0～t2时间内位移相等
如图所示，将质量为m的滑块放在倾角为θ的固定斜面上．滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等，重力加速度为g，则( )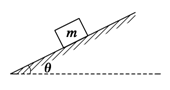
| A．将滑块由静止释放，如果μ>tan θ，滑块将下滑 |
| B．用平行于斜面向上的力拉滑块向上匀速滑动，如果μ＝tan θ，拉力大小应是2mgsin θ |
| C．用平行于斜面向下的力拉滑块向下匀速滑动，如果μ＝tan θ，拉力大小应是mgsin θ |
| D．给滑块沿斜面向下的初速度，如果μ<tan θ，滑块将减速下滑 |
在交通事分析中，刹车线的长度是很重要的依据．刹车线是汽车刹车后，停止转动的轮胎在地面上滑动时留下来的痕迹．在某次交通事故中，汽车刹车线的长度为14m，若汽车的轮胎与地面之间的动摩擦因数为0.7，且g取10m／s2，则汽车开始刹车的速度为（）
| A．7m／s | B．10m／s | C．14m／s | D．20m／s |
如图所示，用绳索将重球挂在墙上，不考虑墙的摩擦。如果把绳的长度增加一些，则球对绳的拉力F1和球对墙的压力F2的变化情况是（）
| A．F1增大，F2减小 | B．F1减小，F2增大 |
| C．F1和F2都增大 | D．F1和F2都减小 |
如图所示，将一个已知力F分解为F1和F2，已知F＝10 N，
F1与F的夹角为37°，则F2的大小不可能是(sin 37°＝0.6,
cos 37°＝0.8)( )
| A．4 N | B．6 N |
| C．10 N | D．100 N |
一质量为m的人站在电梯中，电梯向下运动，加速度大小为
（g为重力加速度）。人对电梯底部的压力为（ ）
A． |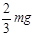
B．2mg | C．mg | D． |