如图线圈abcd面积为0.05m2,共100匝数,线圈电阻为1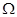 ,外接电阻R=9
,外接电阻R=9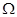 ,匀强磁场的磁感应强度为B=
,匀强磁场的磁感应强度为B=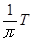 ,当线圈以300rad/min转速匀速旋转时,求:
,当线圈以300rad/min转速匀速旋转时,求: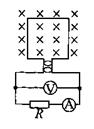
(1)若线圈处于中性面开始计时,写出线圈中感应电动势的瞬时值表达式。
(2)线圈转过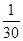 s 电动势的瞬时值为多大?
s 电动势的瞬时值为多大?
一小型发电机内的矩形线圈在匀强磁场中以恒定的角速度ω绕垂直于磁场方向的固定轴转动,线圈的匝数n=100,穿过线圈的磁通量Φ随时间t的变化关系如图甲所示,发电机线圈的电阻r=5Ω,外电路电阻R=95Ω。求串联在外电路中的交流电流表的读数。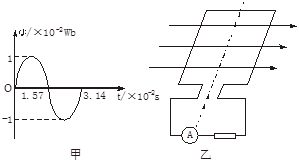
如图所示,矩形线框匝数n=250,ab=12cm,ad=10cm,线框置于B= T的匀强磁场中,绕垂直于磁场的轴OO′以120 r/min 的转速匀速转动,线框通过滑环与外电路相连,外电路接有R="12Ω" 的电阻及一只发光电压和熄灭电压都为12 V的氖泡L。求:
T的匀强磁场中,绕垂直于磁场的轴OO′以120 r/min 的转速匀速转动,线框通过滑环与外电路相连,外电路接有R="12Ω" 的电阻及一只发光电压和熄灭电压都为12 V的氖泡L。求:
(1)当S接e时,电流表读数为多少?R的热功率为多大?10 min内外力对线框做功多少?
(2)当S接f时,氖泡闪光频率为多大?通电10 min,氖泡发光总时间为多少?(线框电阻不计)
一电路如图所示,电源电动势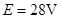 ,内阻
,内阻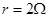 ,电阻
,电阻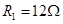 ,
,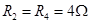 ,
,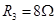 ,C为平行板电容器,其电容C=3.0pF,虚线到两极板距离相等,极板长
,C为平行板电容器,其电容C=3.0pF,虚线到两极板距离相等,极板长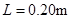 ,两极板的间距
,两极板的间距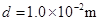 。
。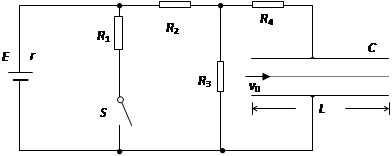
(1)若开关S处于断开状态,则当其闭合后,求流过R4的总电量为多少?
(2)若开关S断开时,有一带电微粒沿虚线方向以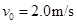 的初速度射入C的电场中,刚好沿虚线匀速运动,问:当开关S闭合后,此带电微粒以相同初速度沿虚线方向射入C的电场中,能否从C的电场中射出?(要求写出计算和分析过程,g取
的初速度射入C的电场中,刚好沿虚线匀速运动,问:当开关S闭合后,此带电微粒以相同初速度沿虚线方向射入C的电场中,能否从C的电场中射出?(要求写出计算和分析过程,g取 )
)
(12 分)如图,质量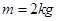 的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经
的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经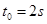 拉至B处。(已知
拉至B处。(已知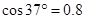 ,
,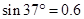 。取
。取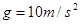 )
)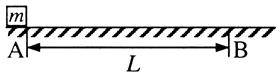
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。