(本小题满分12分)如图1,在直角梯形 中,
中,
 ,
,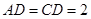 ,点
,点 为线段
为线段 的中点,将
的中点,将 沿
沿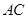 折起,使平面
折起,使平面 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.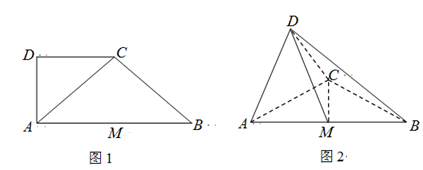
(Ⅰ)求证: 平面
平面 ;
;
【理】(Ⅱ)求二面角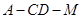 的余弦值.
的余弦值.
【文】(Ⅱ)求点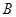 到平面
到平面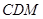 的距离.
的距离.
如图,已知直线l与抛物线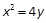 相切于点P(2,1),且与
相切于点P(2,1),且与 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .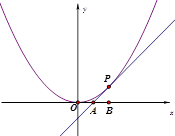
(1)若动点M满足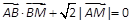 ,求点M的轨迹C;
,求点M的轨迹C;
(2)若过点B的直线l(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
椭圆的对称中心在坐标原点,一个顶点为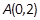 ,右焦点F与点
,右焦点F与点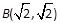 的距离为2。
的距离为2。
(1)求椭圆的方程;
(2)是否存在斜率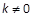 的直线
的直线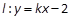 使直线
使直线 与椭圆相交于不同的两点M,N满足
与椭圆相交于不同的两点M,N满足 ,若存在,求直线l的方程;若不存在,说明理由。
,若存在,求直线l的方程;若不存在,说明理由。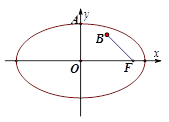
设函数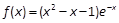 .
.
(1)求f(x)的单调区间和极值;
(2)关于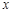 的方程f(x)=a在区间
的方程f(x)=a在区间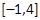 上有两个根,求a的取值范围.
上有两个根,求a的取值范围.
已知抛物线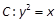 .命题p: 直线l1:
.命题p: 直线l1: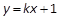 与抛物线C有公共点.命题q: 直线l2:
与抛物线C有公共点.命题q: 直线l2: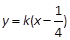 被抛物线C所截得的线段长大于2.若
被抛物线C所截得的线段长大于2.若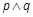 为假,
为假, 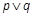 为真,求k的取值范围.
为真,求k的取值范围.
已知圆C过原点且与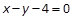 相切,且圆心C在直线
相切,且圆心C在直线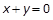 上.
上.
(1)求圆的方程;(2)过点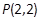 的直线l与圆C相交于A,B两点, 且
的直线l与圆C相交于A,B两点, 且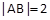 , 求直线l的方程.
, 求直线l的方程.