如图1,A、B两个转盘分别被分成三个、四个相同的扇形,分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).
(1)用列表(或画树状图)的方法,求两个指针所指的区域内的数字之和大于7的概率;
(2)如果将图1中的转盘改为图2,其余不变,求两个指针所指区域的数字之和大于7的概率.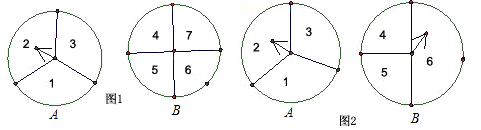
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.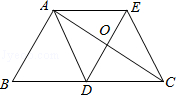
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D在直线上,D的横纵坐标之积为2,过D作两坐标轴的垂线DC、DE,连接OD.
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证:AD•BD为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD="24" cm,BC="26" cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,四边形PQCD是等腰梯形?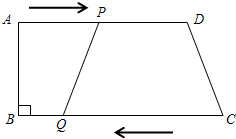
A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?