已知直线 经过点
经过点 ,倾斜角
,倾斜角 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交于两点
相交于两点 、
、 ,求点
,求点 到
到 、
、 两点的距离之和。
两点的距离之和。
(本小题满分12分)
已知定义域为 的函数
的函数 满足:①
满足:① 时,
时, ;②
;② ③对任意的正实数
③对任意的正实数 ,都
,都
有 .
.
(1)求证: ;
;
(2)求证: 在定义域内为减函数;
在定义域内为减函数;
(3)求不等式 的解集.
的解集.
(本小题满分12分)
已知定义在R上奇函数 在
在 时的图象是如图所示的抛物线的一部分.
时的图象是如图所示的抛物线的一部分.
(1)请补全函数 的图象;
的图象;
(2)写出函数 的表达式(只写明结果,无需过程);
的表达式(只写明结果,无需过程);
(3)讨论方程 的解的个数(只写明结果,无需过程).
的解的个数(只写明结果,无需过程).
(本小题满分12分)
已知函数 为偶函数,且
为偶函数,且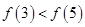 .
.
(1)求m的值,并确定 的解析式;
的解析式;
(2)若
 ,求
,求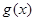 在
在 上值域.
上值域.
(本小题满分12分)计算:
(1)计算 ;
;
(2)已知 ,求
,求 .
.