平行正对极板A.B间电压为U0,两极板中心处均开有小孔。平行正对极板C.D长均为L,板间距离为d,与A.B垂直放置,B板中心小孔到C.D两极板距离相等。现有一质量为m,电荷量为+q的粒子从A板中心小孔处无初速飘入A.B板间,其运动轨迹如图中虚线所示,恰好从D板的边沿飞出。该粒子所受重力忽略不计,板间电场视为匀强电场。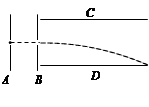
(1)求出粒子离开B板中心小孔时的速度大小;
(2)求出C.D两极板间的电压。
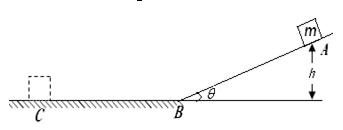
如图所示,光滑斜面的倾角为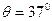 ,可以看成质点的某物体的质量为
,可以看成质点的某物体的质量为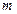 ,物体从距离水平面高为
,物体从距离水平面高为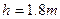 的
的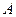 点由静止开始沿斜面下滑,经过
点由静止开始沿斜面下滑,经过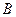 点后进入粗糙的水平地面(设物体经过
点后进入粗糙的水平地面(设物体经过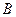 点时速度的大小不变),最后停在
点时速度的大小不变),最后停在 点,已知物体与水平地面的动摩擦因数为
点,已知物体与水平地面的动摩擦因数为 ,试求出物体到达
,试求出物体到达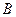 点时的速度大小
点时的速度大小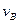 和
和 两点间的距离
两点间的距离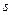 。(已知
。(已知 ,
,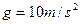 )
)
如图所示,质量为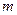 的物体在恒力
的物体在恒力 的作用下,沿着竖直平整的墙壁向下做匀速直线运动,已知恒力
的作用下,沿着竖直平整的墙壁向下做匀速直线运动,已知恒力 与竖直方向的夹角为
与竖直方向的夹角为 ,试求物体与墙壁间的动摩擦因数
,试求物体与墙壁间的动摩擦因数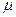 。
。
某人以 的速率跑动去追赶停在路边的公共汽车。当他距离公共汽车
的速率跑动去追赶停在路边的公共汽车。当他距离公共汽车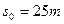 时,公共汽车以
时,公共汽车以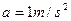 的加速度匀加速启动前进,
的加速度匀加速启动前进,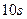 后汽车将匀速运动。试分析讨论人能否追赶上公共汽车?如果能赶上,请求出从汽车开始启动时到人赶上汽车所经历的时间;如果不能赶上,请求出人与汽车之间的最小距离。
后汽车将匀速运动。试分析讨论人能否追赶上公共汽车?如果能赶上,请求出从汽车开始启动时到人赶上汽车所经历的时间;如果不能赶上,请求出人与汽车之间的最小距离。
一个质量为m的木块,从半径为R、质量为M的1/4光滑圆槽顶端由静止滑下。槽可沿着光滑平面自由滑动,如图所示,木块从槽口滑出时的速度大小为多少?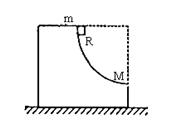
如图所示,在xOy平面内,电荷量为q、质量为m的电子,从原点O垂直射入磁感应强度为B的匀强磁场中,电子的速度为v0,方向与x轴正方向成30°角,试求:
(1)电子从O点开始,第一次到达x轴所用的时间是多少?
(2)电子经过x轴的位置距坐标原点O的距离是多少?