如图所示的电路中,R1=9Ω,R2=30Ω,S闭合时,电压表V的示数为11.4V,电流表A的示数为0.2A,S断开时,电流表A的示数为0.3A,(各表均为理想表)求:
(1)电阻R3的值;
(2)电源电动势E和内阻r的值。
(选做)如图所示,质量为m的物体,从高为h的山坡上 A点由静止开始向下滑到水平雪地上的B点停下来,若将其从B点沿原路拉回A处,至少需做多少功?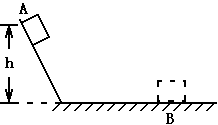
(选做)一个小球从光滑的半球的顶点由静止开始滚下,半球的半径为R,则小球滑至什么位置将离开半球?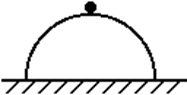
(选做)静止在水平地面上的正立方体木块的边长为a,质量为m。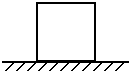
求(1)最小用多大的力可以推翻木块?
(2)推翻木块至少做多少功?
(3)用这种方法使木块移动10m,人对木块做多少功?
(选做)如图所示,轻绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬在绳上O点,O与A、B两滑轮的距离相等,在轻绳的C、D两端分别施加竖直向下的恒力F=mg,先托住物块,使绳子处于水平拉直状态,无初速度地释放物块,在它下落的过程中,保持C、D两端的拉力F不变,不计摩擦。
求(1)当物块下落多大距离时,其加速度为零?
(2)在第(1)的过程中,C端的恒力F做的功多大?
(3)物块下落的最大速度及最大距离各是多大?
物块质量为m,由高H斜面上端静止开始沿斜面下滑,滑至水平面C点处停止,测得水平位移s,若物块与接触面间的动摩擦因数相同,求动摩擦因数。