如图所示为一传送带装置模型，斜面的倾角θ，底端经一长度可忽略的光滑圆弧与足够长的水平传送带相连接，质量m="2kg" 的物体从高h=30cm的斜面上由静止开始下滑，它与斜面的动摩擦因数μ1=0.25，与水平传送带的动摩擦因数μ2=0.5，物体在传送带上运动一段时间以后，物体又回到了斜面上，如此反复多次后最终停在斜面底端。已知传送带的速度恒为v=2.5m/s，tanθ=0.75，g取10m/s2。求：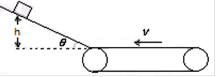
（1）物体第一次滑到底端的速度大小。
（2）从滑上传送带到第一次离开传送带的过程中，求传送带与物体间摩擦产生的热量Q.
（3）从物体开始下滑到最终停在斜面底端，物体在斜面上通过的总路程。
如图，气缸由两个横截面不同的圆筒连接而成，活塞A、B被轻质刚性细杆连接在一起，可无摩擦移动A、B的质量分别为mA＝12kg。mB＝8.0kg,横截面积分别为s1＝4.0×1O-2m2Sg＝2.0×l0-2m2一定质量的理想气体被封闭在两活塞之间,活塞外侧大气压强Po＝1.0×l05Pa
①气缸水平放置达到如图1所示的平衡状态，求气体的压强?
②已知此时气体的体积V1=2.0×10-2m3,现保持温度不变力气缸竖直放置，达到平衡后如图2所示,与图1相比.活塞在气缸内移动的距离l为多少？取重力加速度g＝10m/s2
如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，Y轴为两种场的分界面，图中虚线为磁场区域的右边界，现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置(-L，0)处，以初速度v0沿x轴正方向开始运动，且已知 L=mv02/Eq(重力不计)，试求：
使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d 应满足的条件．
如图所示，长12m质量为50kg的木板右端有一立柱．木板置于水平地面上，木板与地面间的动摩擦因数为0.1，质量为50kg的人立于木板左端，木板与人均静止，当人以4m/s2的加速度匀加速向右奔跑至板的右端时，立刻抱住立柱，(取g=10m/s2)试求：
(1)人在奔跑过程中受到的摩擦力的大小．
(2)人在奔跑过程中木板的加速度．
(3)人从开始奔跑至到达木板右端所经历的时间．
如图所示，AB是粗糙的
圆弧，半径为R，OA水平，OB竖直，O点离地面高度为2R，一质量为m的小球，从A点静止释放，不计空气阻力，最后落在距C点R处的D点。求：
（1）小球经过B点时，对轨道的压力大小。
（2）小球在AB段克服阻力做的功。
如图所示，质量为m的小球自由下落d后，沿竖直面内的固定轨道ABC运动，AB是半径为d的四分之一粗糙圆弧，BC是直径为d的光滑半圆弧，B是轨道的最低点，小球运动到C点对轨道的压力恰为零。求小球在AB圆弧上运动过程中，克服摩擦力做了多少功？