质量M=0.2kg的小圆环穿在固定的足够长的斜木杆上，斜木杆与水平方向的夹角θ=37°，小圆环与木杆间的动摩擦因数μ=0.5，小圆环受到竖直向上的恒定拉力F=3N后，由静止开始沿木杆斜向上做匀加速直线运动（sin37°=0.6，cos37°=0.8，g取10m/s2），求：
（1）小圆环沿斜木杆向上的合外力．
（2）4s末小圆环的速度．
某学校科技兴趣小组，利用废旧物品制作了一个简易气温计：在一个空葡萄酒中插入一根两端开口的玻璃管，玻璃管内有一段长度可忽略的水银柱，接口处用蜡密封，将酒瓶水平放置，如图所示．已知：该装置密封气体的体积为480cm3，玻璃管内部横截面积为0.4cm2，瓶口外的有效长度为48cm．当气温为7℃时，水银柱刚好处在瓶口位置．
①求该气温计能测量的最高气温．
②假设水银柱从瓶口处缓慢移动到最右端的过程中，密封气体从外界吸收3J热量，问：在这一过程中该气体的内能如何变化？变化了多少？（已知大气压为1×105Pa）
有10个相同的木块相互紧挨地放在水平面上，每个木块的质量m=0.4kg，长度L=0.50m，与地面的摩擦系数μ1=0.1，它们原来都静止．另有一质量为M=1.0kg的小铅块，与木块间摩擦系数μ2=0.2，以v0=4.3m/s的水平初速度冲上左边的第一个木块．忽略铅块的大小，试问：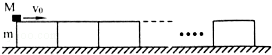
（1）最终整个系统摩擦生热是多少？
（2）通过计算说明铅块是否掉下木块，若能则已，若不能则说明停在那一块木块上？
从地面发射质量为m的导弹，导弹上的喷气发动机可产生恒定大小的推力，导弹起飞时发动机推力大小为F=
mg．导弹沿和水平方向成θ=30°角的直线斜向右上方匀加速飞行．经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转一定角度而大小不变，使导弹依然可以沿原方向匀减速直线飞行．（不计空气阻力和喷气过程中导弹质量的变化，重力加速度为g）求：
（1）推力旋转方向后导弹的加速度的大小？
（2）导弹上升到最高点时离出发点的距离是多少？
如图，轻绳OA一端系在天花板上，与竖直线夹角37°，轻绳OB水平，一端系在墙上，O点处挂一重为40N的物体．（cos37°=0.8，sin37°=0.6）
（1）求AO、BO的拉力各为多大？
（2）若AO、BO、CO所能承受的最大拉力均为100N，则所吊重物重力最大不能超过多大？
如图所示的装置，A物体放置在水平桌面上，右端与跨过定滑轮的细绳相连，A的质量M=2kg，A与桌面间的动摩擦因数μ=0.2，在绳端挂物体B，忽略绳与滑轮、滑轮与轴的摩擦，A物体所受最大静摩擦力与滑动摩擦力认为相等，g取l0m/s2，求：
（1）所挂物体B的质量在什么范围内才能使A保持静止．
（2）当所挂物体B的质量m=0.8kg时，A物体所受摩擦力大小和方向．