(本题共6分)2013年,江阴市某楼盘以每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
如图,抛物线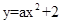 与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,
与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,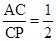 ,且S△AOC=1,过点P作PB⊥y轴于点B.
,且S△AOC=1,过点P作PB⊥y轴于点B.
(1)求BP的长;
(2)求抛物线与x轴的交点坐标.
如图,函数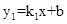 的图象与函数
的图象与函数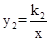 (
(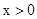 )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).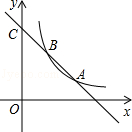
(1)求函数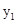 的表达式和点B的坐标;
的表达式和点B的坐标;
(2)观察图象,比较当x>0时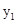 与
与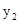 的大小.
的大小.
如图,BC是半圆的直径,AD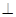 BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.
BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.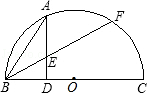
(1)求证:AE=BE;
(2)若点A、F把半圆三等分,BC=12,求AE的长.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=2,AC=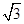 .
.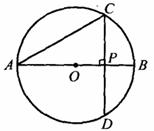
求:(1)∠A的度数;(2)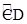 的长;(3)弓形CBD的面积.
的长;(3)弓形CBD的面积.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.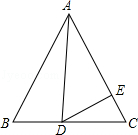
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.