在 中, , ,将 绕点 顺时针旋转一定的角度 得到 ,点 、 的对应点分别是 、 .
(1)当点 恰好在 上时,如图1,求 的大小;
(2)若 时,点 是边 中点,如图2,求证:四边形 是平行四边形.

已知 和点 ,如图.
(1)以点 为一个顶点作△ ,使△ ,且△ 的面积等于 面积的4倍;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设 、 、 分别是 三边 、 、 的中点, 、 、 分别是你所作的△ 三边 、 、 的中点,求证: △ .

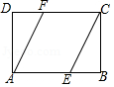
如图,点 、 分别是矩形 的边 、 上的一点,且 .求证: .
如图, 是 外接圆上的动点,且 , 位于 的两侧, ,垂足为 , 的延长线交此圆于点 . ,垂足为 , 交 于点 , , 的延长线交于点 ,且 .
(1)求证: ;
(2)设 外接圆的圆心为 ,若 , ,求 的大小.

求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的 及线段 , ,以线段 为一边,在给出的图形上用尺规作出△ ,使得△ ,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
