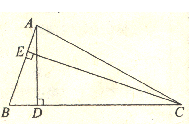
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50º,求∠BAC的度数。
已知直线y=kx-3与x轴交于点A(4,0),与y轴交于点C,抛物线 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍。
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍。(1)求此抛物线的解析式和直线的解析式;
(2)如果点P和点Q同时出发,运动时间为t(秒),试问当t为何值时,△PQA是直角三角形;
(3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大,若存在,求出点D坐标;若不存在,请说明理由。
已知⊙O过点D(4,3),点H与点D关于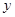 轴对称,过H作⊙O切线交
轴对称,过H作⊙O切线交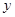 轴于点A
轴于点A
(1)求⊙O半径;
(2)求
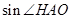 的值;
的值;(3)如图,设⊙O与
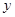 轴正半轴交点P,点E、F是线段OP上的动点(与P点不重合),联结并延长DE、DF交⊙O于点B、C,直线BC交
轴正半轴交点P,点E、F是线段OP上的动点(与P点不重合),联结并延长DE、DF交⊙O于点B、C,直线BC交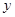 轴于点G,若
轴于点G,若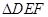 是以EF为底的等腰三角形,试探索
是以EF为底的等腰三角形,试探索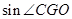 的大小怎样变化?请说明理由。
的大小怎样变化?请说明理由。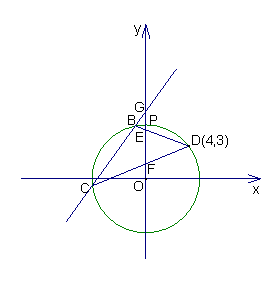
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E。
(1)求∠D的度数;
(2)求证:
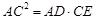 ;
;(3)求
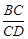 的值。
的值。
已知:如图,在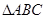 中,
中,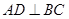 于点D,
于点D,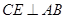 于点E,
于点E,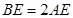 ,
,
且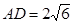 ,
,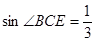 ,求CE的长。
,求CE的长。