如图，在△ABC中，BC=12cm，AB=AC， ∠BAC=120°．
（1）尺规作图：作△ABC的外接圆（只需作出图形，并保留作图痕迹）；
（2）求它的外接圆半径．
为培养学生养成良好的“爱读书、读好书、好读书”的习惯，让书籍成为传递文明、传递知识、传递和谐的载体，哈市某中学计划创建中、小型两类班级图书角打造书香校园，已知组建一个中型图书角需科技类书籍80本，人文类书籍50本，共需购书费用860元；组建一个小型图书角需科技类书籍30本，人文类书籍60本，共需购书费用570元，又知每本科技类书籍的价格相同，每本人文类书籍的价格也相同．
(1)求每本科技类书籍和每本人文类书籍的价格分别为多少元?
(2)若该学校计划用不超过20000元的资金组建中、小型两类图书角共30个，求最多组建多少个中型图书角?
某中学组织全体学生参加了“学雷锋”的活动，六年级一班同学统计了该天本班学生打扫街道，去敬老院服务和到社区文艺演出的人数，并做了如下直方图和扇形统计图.请根据该班同学所作的两个图形解答：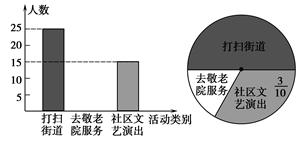
（1）六年级一班有多少名学生?
（2）求去敬老院服务的学生人数，并补全直方图的空缺部分;
（3）若六年级有800名学生，估计该年级去敬老院的人数.
已知矩形ABCD的周长为12，E、F、G、H为矩形ABCD的各边中点，若AB=x，四边形EFGH的面积为y．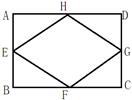
（1）请直接写出y与x的函数关系式；
（2）根据(1)中的函数关系式,计算当x为何值时，y最大，并求出最大值.
（参考公式：当x=-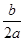
时，二次函数y=ax+bx+c(a≠o)有最小(大)值
）
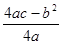如图，在⊙O中，CD为⊙O的直径，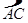
=
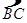，点E为OD上任意一点(不与O、D重合).求证：AE=BE.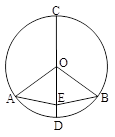
如图1、图2分别是10×6的正方形网格，网格中每个小正方形的边长均为1，线段AB的端点A、B均在小正方形的顶点上.
（1）在图1中以AB为边作锐角三角形ABC，使其为轴对称图形（点C在小正方形的顶点上）（画一个即可）;
（2）在图2中以AB为边作四边形ABDE（非正方形，点D、E均在小正方形的顶点上），使其为轴对称图形且面积为20（画一个即可）.