(本题12分)阅读下列材料并解决有关问题:
我们知道 现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式
现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式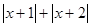 时,可令
时,可令 和
和 ,分别求得
,分别求得 和
和 (称
(称 ,
, 分别为
分别为 与
与 的零点值).在有理数范围内,零点值
的零点值).在有理数范围内,零点值 和
和 可将全体有理
可将全体有理数分成不重复且不遗漏的如下 种情况:(1)
种情况:(1) ;(2)
;(2) ;(3)
;(3) .从而化简代数式
.从而化简代数式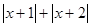 可分以下
可分以下 种情况:
种情况:
(1)当 时,原式
时,原式 ;
;
(2)当 时,原式
时,原式 ;
;
(3)当 时,原式
时,原式 .
.
综上讨论,原式
通过以上阅读,请你解决以下问题:
(1)分别求出 和
和 的零点值;
的零点值;
(2)化简代数式 ;
;
(3)解方程 .
.
自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
某商人开始时,将进价为每件8元的某种商品按每件10元出售,每天可售出100件.他想采用提高售价的办法来增加利润,经试验,发现这种商品每件每提价l元,每天的销售量就会减少10件.
(1)写出售价x(元/件)与每天所得的利润y(元)之间的函数关系式;
(2)每件售价定为多少元,才能使一天的利润最大。
已知方程组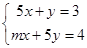 与
与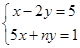 有相同的解,求m2-2mn+n2的值
有相同的解,求m2-2mn+n2的值
小颖家去年的饮食支出3600元,教育支出1200元,其他支出7200元,小颖家今年的这三项支出依次比去年增长了9%,30%,6%,请你帮小颖算一算今年的总支出比去年增长的百分数是多少?
小明这样帮她算的: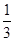 (9%+30%+6%)=15%
(9%+30%+6%)=15%
你认为他这样计算对吗?为什么?
