(15分)如图所示，虚线OC与y轴的夹角θ=60°，在此角范围内有一方向垂直于xOy平面向外、磁感应强度大小为B的匀强磁场。虚线OC与x轴所夹范围内有一沿x轴正方向、电场强度大小为E的匀强电场。一质量为m、电荷量为q的带正电的粒子a(不计重力)从y轴的点M（0，L）沿x轴的正方向射入磁场中。求：
（1）要使粒子a从OC边界离开磁场后竖直向下垂直进入匀强电场，经过匀强电场后从x轴上的P点（图中未画出）离开，则该粒子射入磁场的初速度v1和OP的距离分别为多大？
（2）若大量粒子a同时以
从M点沿xOy平面的各个方向射入磁场中，则从OC边界最先射出的粒子与最后射出的粒子的时间差。
在图所示的电路中，电源的电动势E =" 6.0" V，内电阻r =" 1.0" Ω，外电路的电阻R =" 5.0" Ω. 闭合开关S.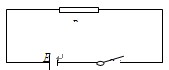 
求：（1）通过电阻R的电流Ⅰ
（2）电阻R消耗的电功率P.
电场中某区域的电场线如图所示， A、B是电场中的两点. 一个电荷量q = +4.0×10-8 C的点电荷在A点所受电场力FA=2.0×10-4 N，将该点电荷从A点移到B点，电场力做功WAB= 8.0×10-7J .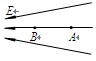 
求：（1）A点电场强度的大小EA
（2）A、B两点间的电势差UAB.
一根长为0.20m的直导线，垂直于某匀强磁场方向放置，当导线中通有1A的电流时，导线受到的安培力大小为0.08N，则：
（1）磁场的磁感应强度为多大？
（2）当导线中的电流增大为2A时，导线受到的安培力为多大？此时磁场的磁感应强度为多大？
如图所示，有一U形金属导轨MNPQ，处在与它垂直的匀强磁中.有一导体棒ab在导轨上向右匀速运动，经过0. 1 s，从“1”位置运动到“2”位置.这个过程中，穿过由导轨和导体棒组成的闭合回路的磁通量从0.05Wb增加到0.15Wb。
求：(1)这段时间内通过回路的磁通量的变化量；
（2)这段时间内线圈中的感应电动势的大小。
(13分)劫匪驾车在一条平直公路上以40m/s匀速行驶，当劫匪车经过停在路边的警用摩托车旁时，车上警察开枪击坏匪车使匪车匀减速直线行驶，3秒后启动警车匀加速行驶追赶匪车，已知警车起动的加速度为1m/s2,匪车减速行驶的加速度为4m/s2。
求：(1)警车刚启动时，匪车的速度大小和此时两车相距多远？
(2)警察开枪后多少时间追上匪车？