如图所示,三个质量分别为3kg、1kg.1kg的木块A.B、C放置在光滑水平轨道上,开始时B、C均静止,A以初速度v0=5m/s向右运动,A与B碰撞后分开,B又与C发生碰撞并粘在一起,此后A与B间的距离保持不变.
①求B与C碰撞前B的速度大小;
②若A与B的碰撞时间约为0.01s,求B对A的作用力F.
如图(a)所示,在倾角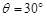 的光滑固定斜面上有一劲度系数k=100N/m的轻质弹簧,弹簧下端固定在垂直于斜面的挡板上,弹簧上端拴接一质量m=2 kg的物体,初始时物体处于静止状态。取g=10 m/s2。
的光滑固定斜面上有一劲度系数k=100N/m的轻质弹簧,弹簧下端固定在垂直于斜面的挡板上,弹簧上端拴接一质量m=2 kg的物体,初始时物体处于静止状态。取g=10 m/s2。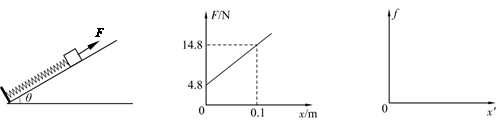
(a)(b)(c)
(1)求此时弹簧的形变量x0;
(2)现对物体施加沿斜面向上的拉力F,拉力F的大小与物体位移x的关系如图(b)所示,设斜面足够长。
a.分析说明物体的运动性质并求出物体的速度v与位移x的关系式;
b.若物体位移为0.1m时撤去拉力F,在图(c)中做出此后物体上滑过程中弹簧弹力f的大小随形变量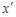 的函数图像;并且求出此后物体沿斜面上滑的最大距离xm以及此后运动的最大速度vm。
的函数图像;并且求出此后物体沿斜面上滑的最大距离xm以及此后运动的最大速度vm。
质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体,半径为R。
(1)已知地球质量为M,自转周期为T,引力常量为G。求此时卫星对地表的压力N的大小;
(2)卫星发射后先在近地轨道上运行(轨道离地面的高度可以忽略不计),运行的速度大小为v1,之后经过变轨成为地球的同步卫星,此时离地面高度为H,运行的速度大小为v2。
a.求比值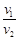 ;
;
b.若卫星发射前随地球一起自转的速度大小为v0,通过分析比较v0、 v1、v2三者的大小关系。
某游乐设施如图所示,由半圆形APB和直线BC组成的细圆管轨道固定在水平桌面上(圆半径比细管内径大得多),轨道内壁光滑。已知APB部分的半径R=0.8 m,BC段长L=1.6m。弹射装置将一质量m=0.2kg的小球(可视为质点)以水平初速度v0从A点弹入轨道,小球从C点离开轨道水平抛出,落地点D离C点的水平距离为s=1.6m,桌子的高度h=0.8m,不计空气阻力,取g=10m/s2。求: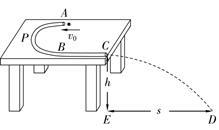
(1)小球水平初速度v0的大小;
(2)小球在半圆形轨道上运动时的角速度ω以及从A点运动到C点的时间t;
(3)小球在半圆形轨道上运动时细圆管对小球的作用力F的大小。
1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验,这次实验的目的是要发展一种技术,找出测定轨道中人造天体质量的方法。实验时,用双子星号宇宙飞船m1 去接触正在轨道上运行的火箭组m2(后者的发动机已熄火)。接触以后,开动双子星号飞船的推进器,使飞船和火箭组共同加速(如图所示)。推进器的平均推力F等于895 N,推进器开动时间为7s,测出飞船和火箭组的速度变化是0.91 m/s。已知双子星号宇宙飞船的质量m1=3400 kg。求: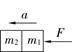
(1)飞船与火箭组的加速度a的大小;
(2)火箭组的质量m2。
一物体静止在光滑水平面上,某时刻起受到水平面内两个互相垂直的恒力F1、F2的作用(俯视图如图所示),物体的位移大小x=1m。已知F1=6N,F2=8N。求:
(1)合力F的大小和方向;
(2)F1对物体所做的功W1以及F对物体所做的功W。